Do the Galilean moons' orbits around the Sun have loops (i.e. have concave parts)? And if so, how can their orbits be graphed?

Question

The shape of the Moon's orbit around the Sun has been discussed to death, and the answer is that the Moon's orbit has no concave "loops" whatsoever.

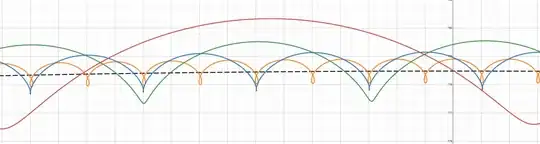
I am relatively sure that the determinant factor in whether a moon has a "concave" orbit with loops or a loop-less orbit has to do with its orbital velocity. If the moon orbits its planet faster than the planet orbits the Sun, then the moon has the intuitively-expected looped orbit. If not, then it is loopless.

From my calculations, Io and Europa orbit Jupiter faster than Jupiter orbits the Sun, while Ganymede and Callisto orbit slower than Jupiter orbits the Sun. Therefore, it's expected that Io and Europa make loops around Jupiter while it is orbiting the Sun, while Ganymede and Callisto don't.

This is all great, except I have no clue how to verify this hypothesis. I originally thought the only way to see was to run a simulation, however I'm 90% sure it can be done by graphing parametric equations using WolframAlpha or Desmos.

One problem: I have exactly zero idea how to go on doing that, and barely know parametric equations exist to begin with. So if someone smarter than me could graph the Galilean moons' orbits and verify if Io and Europa have loops while Ganymede and Callisto don't, I'd appreciate it.

Answer 1

Compare the orbital speeds and use the superposition.

Jupiter's orbital speed around the sun is around 13km/s. Io's speed around Jupiter is around 17km/s. So it will actually go backwards.

For plotting also apply the superposition principle of the motions.

How to create such plot: Assuming that the moon has a circular orbit with period T_m, you can describe its motion in cartesian coordinates as $x_m(t) = r_m\cdot\sin(2\pi t/T_m) $ and $y_m(t) = r_m\cdot\cos(2\pi t/T_m) $. Add to that the movement of Jupiter with its orbital period of $T_J = 12$years and distance $r_J$ around the sun: $x_J(t) = r_J\cdot\sin(2\pi t/T_J) $ and $x_J(t) = r_J\cdot\cos(2\pi t/T_J) $. Calculate x and y for small time steps (probably hours or even minutes, given the moon's small orbital period of a few days), but cover a complete orbit around jupiter and plot the resulting positions.

I cannot plot right now with my phone. But @MikeG meanwhile plotted it: where the black dashed line is Jupiter's orbit around the Sun, and orange, blue, green and red are the orbits of Io, Europa Ganymede and Calisto respectively using these data.

Additionally, this Desmos plot shows the orbits of all large round moons around their respective planet, assuming circular orbits. Note that some satellites' orbits (namely Enceladus and Dione) might appear janky; zooming out or in might fix the issue.

In summary: Io, Europa, Mimas, Enceladus, Tethys, and Dione are the only large round moons that have “loops” in their orbits. All other large satellites have no retrograde part in their orbit with respect to the Sun, including Ganymede and Calisto as shown in the plot above. Convex is a stricter criterion than "not retrograde" and geometrically means that I can take any arbitrary point on the orbit and reach on a straight line any other point of the orbit and remain within the area encircled by the orbit. Mathematically it means that the sign of the curvature of the orbit around the Sun does not change. Looking at the moons' orbits, the geometrical explanation of concave makes it immediately clear that none of them is a concave orbit.