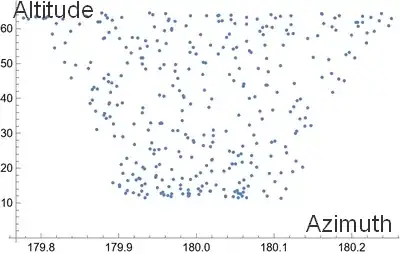
This isn't libration.
The moon's average rotation matches exactly to its orbital period, so it always shows the same face towards Earth, but there is a slight "wobble" and you can see up to about 5 degrees around the "back" of the moon.
What you are plotting cannot be the position at the moment of transit, since by definition this is at 180 degrees and all you points would be in a vertical line in the middle.
Your plot coulds be the position of the moon above the horizon at the point when it reaches its highest point. This will always be very close to culmination (which is when the moon is at exactly 180 degrees, due south) but could be very slightly different, due to the fact that the moon is also moving along the ecliptic, which may be tilted to the horizon. (Or it could be some other source of error in the Mathematica data)
So the highest point can be a few tenths of a degree different to due south. This effect would be greater when the moon is higher, as the meridians are closer together near the zenith than near the horizon. This explains the trapezium-shaped distribution of points.