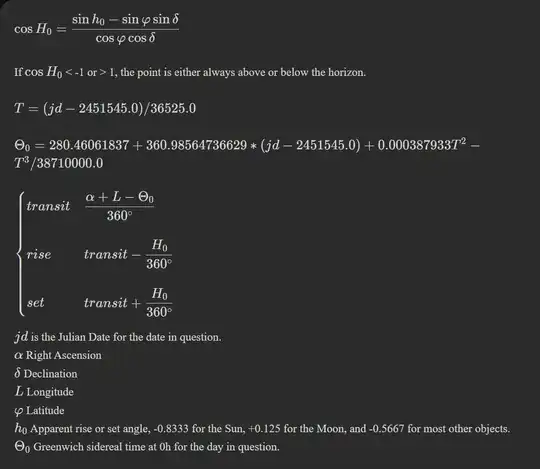
I'm trying to develop an Excel macro to compute when a target will rise above a specified altitude given the date and location. I can get the correct answer with Stellarium and using a Python program I wrote that leverages the PyEphem library, but for some reason I cannot get the right answer when I try to implement the calculations myself using Excel. I'm hoping someone can point out the error of my ways.
These are the input variables:
Date: 10/18/2023
Altitude: 30°
Target: M74
RA: 01:36:43.1
Dec: +15° 47' 08"
Location:
Lat: 32° 36' 50"
Long: -116° 20' 01"
According to Stellarium and the Python program using PyEphem, the correct answer is 20:16:55 PDT (03:16:55 UTC the following day). But I cannot arrive at the same answer and don’t know where I’m going wrong.
As I understand it, the steps are as follows:
Compute the LHA
Cos(LHA) = [SIN(Alt) - SIN(Lat) * SIN(Dec)] / (COS(Lat) * COS(Dec))
Cos(LHA) =[0.5 - 0.538974977 * 0.272037656] / (0.842321776 * 0.962286607)
Cos(LHA) = 0.435971065
LHA = Acos(0.435971065) = 1.119679324 rad = 64.2° = 4.276860089 hours = 04:16:37
This result is close to the LHA for M74 in the western sky according to Stellarium (04:16:54). Subtracting that value from 2*Pi to get the LHA when M74 is in the eastern sky, we get:
5.163505973 rad = 295.8° = 19.72 hours = 19:43:23 (Stellarium has 19:43:05)
I’m not sure why there is a difference of 17-18 seconds, but it’s close enough that I’m comfortable with the answer.
Compute the LST
LST(E) = LHA(E) + RA = 5.163505973 + 0.422013334 = 5.585519307 rad = 320.0° = 21.34 hours = 21:20:06
Stellarium has 21:20:58.5 for the Apparent Sidereal Time so the difference is now 52 seconds, but again, it seems close enough to be on the right track.
Compute the GMST
GMST(E) = LST(E) – Long = 5.585519307 – (-2.03040451) = 7.61592393525783
That value is greater than 2Pi; do I need to subtract 2Pi or leave it as is?
Then, using the Meeus formulas, we have:
JD0 = 2460235.5 (for 10/18/2023)
T = (JD0 - 2451545) / 36524.22 = 0.237938003877975
UT = (GMST(E-hours) - 6.697374558 - 2400.051336 * T - 0.000025862 * (T * T)) / 1.0027379093
UT = -547.172006240208 Mod 24 = 4.82799375979209 = 04:49:41
LT (PDT) = UT – 7 = 21:49:41
That answer is incorrect by over 1-1/2 hours; Stellarium and PyEphem both show the correct time should be 20:16:54 PDT
It appears that the calculations are correct through Step 3, but it goes awry sometime during Step 4. Can anyone see where I’m getting off track?