As a supplement to @ProfRob's answer.
The answer there only takes into account the leading order contribution coming from $\ell=m=2$ quadrupole mode. For binaries that are far from merger, and merging equal mass (non-spinning) black holes this is by far to most dominant mode, but for unequal mass binaries in the strong field the situation can be quite different.
In the general, the distribution of the gravitational wave strain along the celestial sphere can be written:
$$ h(\Theta_{\rm obs},\Phi_{\rm obs}) = \sum_{\ell=2}^\infty\sum_{m=-\ell}^m h_{\ell m} {_{-2}}Y_{\ell m}(\Theta_{\rm obs},\Phi_{\rm obs}),$$
where the $ {_{-2}}Y_{\ell m}$, are so called spin-weighted spherical harmonics, the $h_{\ell m}$ are the referred to as the multipole modes.
As mentioned above, typically the $h_{22}$ is by far the largest mode, but all modes are emitted in any particular gravitational event, unless there is additional symmetry (such as in a head on collision). However, you can deviated quite far from the standard picture. Below is a graphic representation of the GW strain distribution caused by a small-mass orbit a Kerr black hole with near extremal spin ($a=0.995GM/c^2$) on the innermost stable circular orbit (ISCO), obtained as an approximation linear in the mass of the smaller object,
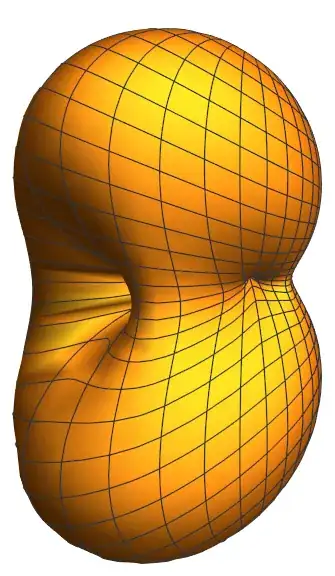
The $\ell=m=2$ mode is still the largest contribution, but the $\ell=m=3$ and other $\ell=m=4$ modes are very close. The consequence is that the maximal strain is not obtain "face-on" ($\Theta_{\rm obs}=0$), but at viewing angle of $\Theta_{\rm obs} \approx 42.9$ degrees.
