5

Using PyEphem, I calculated the time difference between consecutive summer solstices in the south hemisphere for the last 4000 years, and plotted them in a graph. It seems like random noise around the mean, but the amplitude seems to oscilate with a period of around ~161 years. What explains this behavior?

enter image description here

Code used:

import ephem

date = ephem.Date("2023/01/01")
solstice = ephem.previous_winter_solstice(date)
for i in range(4000):
    previous_solstice = ephem.previous_winter_solstice(solstice)
    print(solstice - previous_solstice)
    solstice = previous_solstice
ordptt
  • 173
  • 1
  • 5
  • 1
    I suspect that it's due to some cycle involving the Moon, similar to what happens with perihelion & aphelion, as I explained here. – PM 2Ring Jun 04 '23 at 15:44
  • 1
    OTOH, just playing with various mean month & year lengths I can't make a simple 161 year cycle. The best I can do is 239 years, just under 1½ of your cycles. Roughly, 2956 synodic months = 3168 anomalistic months = 239 tropical years = 87293 days. https://sagecell.sagemath.org/?z=eJxVjs0OgyAQhO8kvMMetSGmgovQpM9ijNqUWH4CXPTpS20Pdg9z2G8yM9a7_BzS5vxsJrgD1w2KKyqlZEuJPejovB1fH9g3iB12ulBKtmWMQ44-mOmgQmLDO94q3VMSlmj8nMrbnhsYnCMZ_GVQkoou6ZiBkoFopWLAhabk4SOsDDIYB7sJ1dfJ4NdT3yiBciEal6sVLpDrN873Qm8=&lang=python – PM 2Ring Jun 04 '23 at 15:45
  • 2
    The paper Fedorov, V.M. "Interannual variations in the duration of the tropical year." Seems to be about this. The abstract says that it is due to "perturbations" but the article is behind a paywall. – James K Jun 04 '23 at 16:15
  • 1
    If I include the synodic period of Jupiter (398.88404 days), then I get 6011 synodic, 6442 anomalistic, 445 Jupiter, 486 Tropical ~= 177508 days, which is intriguing. ;) – PM 2Ring Jun 04 '23 at 16:17
  • 1
    FWIW, I used the LLL algorithm from the answer to your old question: https://math.stackexchange.com/q/4412720/207316 – PM 2Ring Jun 04 '23 at 16:37
  • 1
    You should probably add a little more detail to this question. What time scale are you using (UTC, Terrestrial Time, JPL's TDB, etc)? What exact definition for solstice are you using? Maybe post your Python code, or at least a minimal version that people can use to reproduce your results. – PM 2Ring Jun 04 '23 at 16:37
  • 1
    @PM2Ring I edited to include the code I used.

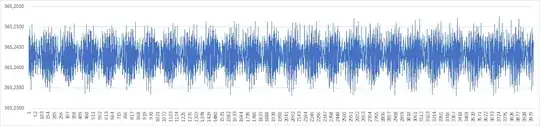
    With regard to finding a cycle that is close to 161 years, the only one I was able to find is the orbital period of Neptune, but it most certainly doesn't have any influence on the tropical year.

     – ordptt Jun 04 '23 at 19:18
  • 3
    @JamesK: I have read the article, but it mentions no 161-year period. I suspect, as PM 2Ring does, that it has to do with Moon cycles. Multiplying the apsidal precession period (8.61 years) by the nodal precession period (18.6 years) gives 164.61 years, which is close to 161 years… – Pierre Paquette Jun 04 '23 at 22:14
  • Check the algorithm used to compute it. Generally the solstice accounts for precession, but not nutation. So you're likely looking at combined effects of precession and Earth's orbit. So, to find the source, you'd want to remove one of those variables. I doubt the result would be anything other than "the math just happens to produce that pattern". – Greg Miller Jun 05 '23 at 03:32
  • @GregMiller Comparing the solstice times of the algorithm with other sources, they agree within the minute, the difference usually being of a couple of seconds. The variations in the graph are of several minutes, so I tend to think it is not related to an imprecision of the algorithm. – ordptt Jun 05 '23 at 14:13
  • The 161 year cycle is consistent with Fedorov's paper which notes a decreased variation in the years 1960-2000, but since their Figure 2 only looks at 150 years they don't see the full cycle. The cycle is visible in the 400 years accessible from the US Naval Observatory at https://aa.usno.navy.mil/data/Earth_Seasons. The cycle occurs for all solstices and equinoxes, but shifted by 40 years for each step as you go from summer to fall to winter to spring. e.g. When the variations are largest in the summer-solstice "year", they are smallest in the winter-solstice "year". – David Bailey Jun 13 '23 at 20:56

0 Answers0