1

I built a calculator to calculate a planet's atmospheric pressure at an altitude with the formula below.
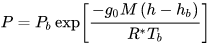
P = P₀ • e(-gM(h-h₀))/(R₀ • T₀)

How does greenhouse effect relate to the formula above? How to calculate it?

I compared the results with the in-game data including same input data but it becomes less accurate the farther it is from sea level so something might be missing behind the scenes.

Heres the ingame data:
3 4

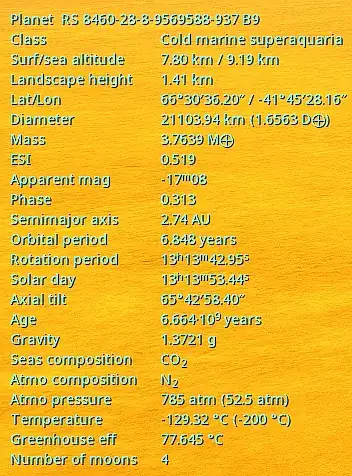
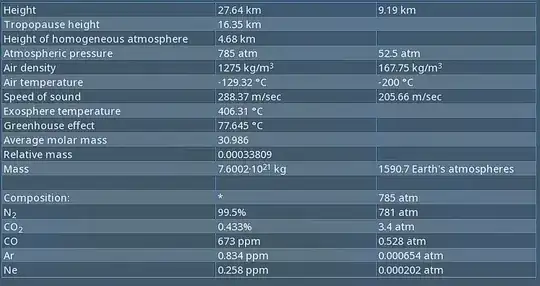
And my calculator results:
5 6

As you can see, the atmos pressure in the in-game data and calculator are not reasonably close enough, maybe I could accept at least around ±1

I searched and asked some people about greenhouse effect on atmospheric pressure

Greenhouse effect isn't directly related to pressure. It's indirectly related to the partial pressure of greenhouse gases

The most direct thing you could relate it to is the optical depth of the atmosphere in infrared (going as optical depth to the 1/4th power), but calculating optical depth from composition and pressures isn't straightforward either.

At the most basic and as a learning tool, they're often treated as a surface + single layer with incoming radiation acting independently of re-emitted radiation. For more complexity, have multiple layers. For more complexity, treat each volume element and its emission in terms of solid angle and each tiny bit of wavelength.

Apparently, the game was more of an emulator rather than a simulator, it could just make up data to make it seem believable and consistent with findings instead of full calculations.

Other possible factors could be lapse rate (the formula above is the version that implies that lapse rate is 0) or Stefan-Boltzmann's Law/black-body radiation/effective temperature.

bridgeofdata
  • 11
  • 2
  • 1
    "I compared the results with the in-game data" what in-game data? You haven't introduced what you are referring to. Also who do you quote in your quotes? Beyond that, i agree with the middle comment you quote - you need at least to know the optical depth of the atmosphere of the outgoing radiation, and how $T_{\rm surface}$ reacts to those optical depth changes (Milne's temperature solution). Then you can plug that into your hydrostatic expression. It's not going to be a sensible model that has reproductive power, but it will give some basic physics correctly. – AtmosphericPrisonEscape Jan 30 '23 at 14:20
  • Thank you for your answer. The in-game data are stats of a planet object like temp, atmos pressure, current height, height above sea level, albedo. Looks like I need to find out the outgoing radiation next.

    How about lapse rate, is it involved?

     – bridgeofdata Jan 31 '23 at 02:19
  • https://link.springer.com/article/10.1007/s40324-021-00265-y#Sec24 Am i reading the right article? – bridgeofdata Jan 31 '23 at 15:43
  • 2
    This paper is specifically only looking at radiatively non-diffusive regions of the atmosphere and is hence incapable of modelling the greenhouse effect of the troposphere. For that you'd need a radiative-convective model. I recommend https://ui.adsabs.harvard.edu/abs/2010A%26A...520A..27G/abstract (and their Eqn. 27) for a conceptual understanding and further https://ui.adsabs.harvard.edu/abs/2012ApJ...757..104R/abstract for a radiative-convective model, that looks sensible in comparison with solar system planets. Then you only need real opacity data to compute $\tau$&$\gamma$. – AtmosphericPrisonEscape Jan 31 '23 at 16:25
  • If you want a deep-dive into what it required to find a sensible model explaining the Earth's temperature structure, have a look at this online book: https://history.aip.org/climate/index.htm and the section "Simple models", it explains the research history in the 1960s nicely. Particularly interesting for you might be the parts about when convection comes in (your quoted lapse rate) to explain why the greenhouse effect isn't even stronger than initially thought (like when you'd apply the Guillot2010 model). In the end, it all comes down to how accurate you want to be. – AtmosphericPrisonEscape Jan 31 '23 at 16:33
  • In the paper you've cited, you can find Eqn. 76 as what is often referred to as THE Milne solution in planetary climate solutions. – AtmosphericPrisonEscape Jan 31 '23 at 17:34
  • https://i.gyazo.com/b18b0e4f9250d2881a0c78377a7b1d60.png
    Why is vibrational degree of freedom counted in N value for CO₂ but not like other N₂, O₂ and other similar molecules? And how did they get γ = 1.3 with 7, I calculated that it has to be around 9.0-9.1. In the first place, its my first time learning about degrees of freedom. I also just figured out what linear molecule is.     – bridgeofdata Feb 01 '23 at 15:01
  • You're trying to dive very deep here. Are you trying to reproduce planetary temperatures 100% correctly (spoiler: you won't without a PhD in physics), or are you trying to build a simplified model for your game that catches the basic greenhouse physics (I would recommend that)? – AtmosphericPrisonEscape Feb 01 '23 at 15:03
  • @bridgeofdata I would guess that the difference in degrees of freedom for the molecules has to do with the fact that N${2}$ and O${2}$ are symmetric (as well as linear), while CO${_2}$ is not. – Peter Erwin Feb 01 '23 at 20:25
  • @PeterErwin thanks for answering – bridgeofdata Feb 02 '23 at 01:17
  • @PeterErwin CO2 is linear and symmetric. The differences at 300K must be in the different electronic binding energies of $C=O$ vs $N-=N$ and $O=O$, such that those vibrational modes are not excited. – AtmosphericPrisonEscape Feb 02 '23 at 02:36
  • @AtmosphericPrisonEscape yea a simplified model would be best, but the 1st linked paper i cant understand whats happening, the 2nd seems easier to understand.
    From my questions & answers, you definitely know that I don't have anything in physics except the basics.     – bridgeofdata Feb 02 '23 at 13:19
  • @bridgeofdata: Then use Eqn. 27 in Guillot's 2010 paper, and the only thing to determine is the optical depth $\tau$ of the greenhouse gas mix, which can be drastically approximated as $\tau = R_p (n_1 \kappa_1 + n_2 \kappa_2 + ....)$, where $R_p$ is the planet radius, the $n_1, n_2, ..$ are abundances $[1/m^3]$ of all greenhouse species, and the $\kappa_1 ...$ are the mean Rosseland opacities, or cross-sections of each species in $m^2/kg$. That's the simplest model possible. – AtmosphericPrisonEscape Feb 02 '23 at 13:29
  • @AtmosphericPrisonEscape Yes, you're right, of course. I think the issue is that there are more distinct ways for a triatomic molecule like CO${2}$ molecule to vibrate than for a diatomic molecule like N${2}$ or O${2}$. https://en.wikipedia.org/wiki/Degrees_of_freedom(physics_and_chemistry) – Peter Erwin Feb 02 '23 at 22:23
  • Eqn. 27 without any input can solve itself? Cancelled out T^4 and got 2/3 for τ. What does this mean?

    Does 1/m^3 for abundance mean 1 atom or mol per cubic metre?

     – bridgeofdata Feb 03 '23 at 09:53
  • How do I get a cross section of an atmosphere? And also, I am stuck on how to get intensity, wavelength and its own opacity to plug into the Rosseland mean opacity formula.

    Edit: I got some progress on calculating abundances, now only the mean opacity left

     – bridgeofdata Feb 04 '23 at 16:25
  • Update: going to read a textbook instead because i need more background knowledge – bridgeofdata Feb 06 '23 at 12:11

0 Answers0