If we were in an earthlike planet at 1AU from a black hole merger, would we be able to hear the spacetime strains as the black holes orbit around each other? How would it sound?
-
1Cool question! A different but related one in Physics SE: How would a passing gravitational wave look or feel? – uhoh Nov 27 '22 at 22:07
-
1Of course, there are some technical difficulties in having an Earth-like planet 1 AU from a pair of merging black holes. ;) It needs a heat source, otherwise its atmosphere will be frozen solid. – PM 2Ring Nov 28 '22 at 02:43
1 Answers
What would be heard is vibrations set up by the gravitational wave in the atmosphere, although presumably they would also directly stimulate the parts of the ear too.
The amplitude of gravitational waves fall off as $1/r$. The proportional change in lengths near (e.g. about a Schwarzschild radius $R_S$ away) the merger is $\approx 1$. So at 1 AU it would be $R_S$/1 AU. For stellar mass black holes this makes the amplitude $\delta\approx 3\cdot 10^{-8}$.
But if we think in terms of sound pressure, the pressure in dB is $20 \log_{10}(P/P_0)$ where $P_0$ is the reference power 20 μPa in air. How do we get a pressure from displacements? This Wikipedia page gives an expression in terms of the acoustic impedance: $P=\delta Z$. Normally this is about 413.3 Pa s/m in 20 degree air, which would give us -4.2 dB for the stellar mass black holes. Which is below the threshold of hearing.
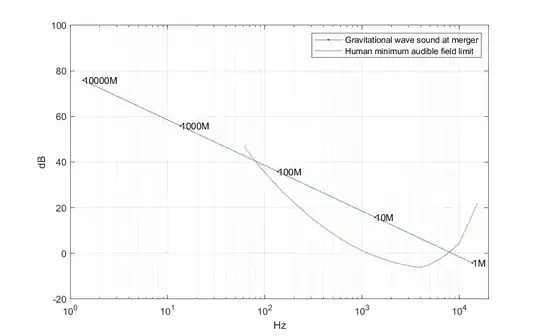
If we instead use $R_S=0.08$ AU for a Sgr A* mass hole pair, now we get 124 dB! That ought to be noticeable... beside the other effects of the merger.
Generally the frequency rises, going up in a chirp, followed by a quick ringing. But the time from the sound becomes noticeable and the merger is likely very quick. Heavy holes merge fast, light ones merge slowly but would be too quiet. However, as Emil pointed out, the frequency is very low for supermassive black holes, maximally about $10^{-2}$ Hz which is below the hearing limit. Stellar mass holes can reach hundreds of Hz, but as discusses above are too quiet at 1 AU.
However, for hole pairs with a combined mass between a few and 200 solar masses the sound intensity does get above the human hearing limit!
- 14,791
- 1
- 35
- 53
-
1perhaps even louder (underwater) than whales!? How much power and energy is (actually) in a 230 dB "click" from a whale? – uhoh Nov 28 '22 at 00:09
-
2One problem with the example of a Sag A* mass hole pair is that the merger frequency at the end of the chirp would probably be too low to be perceived as sound (in the order of mHz, so minutes per cycle or more). – Emil Nov 28 '22 at 11:02
-
1
-
4So stellar mass is the right pitch but too quiet; Sag A* is the volume of a rock concert but too low in pitch. Is there a mass somewhere in between where it's both loud enough and high enough in frequency to be audible? – N. Virgo Nov 29 '22 at 03:42
-
1@N.Virgo - Thanks for making me check! I have added a plot versus a measurement of the human hearing limit. It does look like there is a mass interval where it can be heard! – Anders Sandberg Nov 30 '22 at 00:22