7

Wikipedia says that a synodic month has a length 29 d 12 h 44 min and 2.9 s. I'm interested to find out how often a full moon (but actually, it's the same for any phase) happens during a weekend.

I thought:

  • a weekend lasts 48 h
  • a week has 168 h
  • a synodic month has 708.75 h

But I'm not able to calculate when the full moon happens inside the window of the 48 h we call "weekend".

Mark
  • 359
  • 1
  • 7
  • 2
    Are you asking "What fraction of full moons occur on the weekend", or "What fraction of weekends have a full moon". The answer will be different. Or are you asking something else? – James K Sep 10 '22 at 21:50
  • @JamesK I can rephrase my question in this way: how much weeks (in average) should I wait to have another full moon on the weekend? – Mark Sep 11 '22 at 09:53
  • Is Friday evening not part of the weekend for you? That's unfortunate. – Toby Speight Jan 26 '23 at 07:13

3 Answers3

22

Exactly 2/7 of time is "weekend", There is no exact alignment of the lunar orbit to the length of a week, so a full moon is equally "likely" to be at the weekend

So 2/7 of full moons occur at the weekend. As the synodic month is about 29.5 days there are about 1245 New Moons per century, so you'd get about 356 on the weekend. This full moon (10th Sept) is on Saturday, and next full moon, 9th October 2022 is on Sunday (at my location)

However the moon appears full for a couple of days on either side of the moment at which its longitude is 180° relative to the Sun. This being the case, the moon will appear full at the weekend if it is exactly full on any day between Thursday and Tuesday - which means that most months will have a moon that looks full at the weekend.

Now to think about this in a different way, in a century there are 5218 weekends (±1) and 356 are "full moon weekends", so about 6.8% of weekends are full moon weekends, or to put it another way 1 weekend in 14.66 is a full moon weekend.

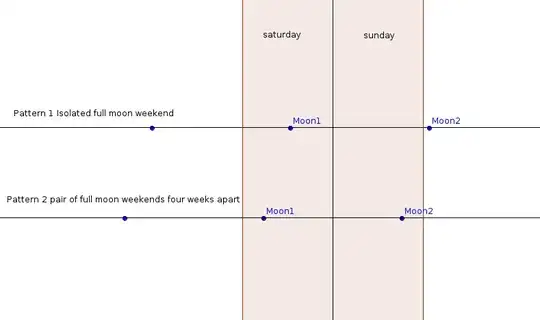
On average, you need to wait for 14.66 weeks before you get another full moon weekend. But this is an average: the pattern of full moon weekends is not at all random. In fact what tends to happen is that there is one full moon weekend, followed four weeks later by second one. Then a gap of more than 14 weeks, before the pattern almost repeats.

So (in my location) there is a full moon on Saturday 10th Sept and Sunday 9th Oct. Then it proceeds: Tuesday in Nov, Thursday in Dec, Friday in Jan, then Sunday 5th February. That is 17 weeks after the October full moon weekend.

Thus, final answers: 2/7 of full moons are at the weekend. 2/29.530588 = 6.8% of weekends have a full moon.

Toby Speight
  • 495
  • 3
  • 11
James K
  • 120,702
  • 5
  • 298
  • 423
  • "2/7 of full moons occur at the weekend". That is non-intuitive for me. Are you saying the length of the synodic month does not matter here? If the moon phases would require 25 days, 31 or whatever, it would be the same then? – Mark Sep 10 '22 at 19:25
  • 11
    Yes. Imagine you have a bag with 200 red counters and 500 blue ones. You spread them out in a line and take every 25th counter. You'd get 2/7 red and 5/7 blue. What if you took every 31st counter? You'd get 2/7 red and 5/7 blue. It is the same with moon phases. – James K Sep 10 '22 at 19:32
  • @Mark That number from Wikipedia is the mean synodic month length. The Moon's motion is rather complex, so there's quite a bit of variation in the actual month length. Fred Espenak says here that "the length of any one synodic month can vary from 29.26 to 29.80 days due to the perturbing effects of the Sun's gravity on the Moon's eccentric orbit". – PM 2Ring Sep 10 '22 at 19:49
  • 2
    Though if the synodic month was 31 days, there would be fewer full moons in a century, and so fewer full moons on the weekend. – James K Sep 10 '22 at 19:57
  • Nice, though unsourced answer. The equal probability assumption is intuitive and we all assume it's true, but I'd love to see a supporting source for it. I haven't a clue to where to look for one though, so I've just asked min Math SE histogramming phases between a periodic function and another periodic, quasiperiodic or almost-periodic function with irrational period relationship. – uhoh Sep 10 '22 at 23:40
  • This answer cuts the Gordian knot of the problem. Well done. – Wastrel Sep 11 '22 at 15:47
  • The length of the synodic month does not matter to the questions of whether a randomly-chosen full moon occurs on a weekend or whether a randomly chosen weekend will have a full moon, but it does matter to questions such as the OP expressed in comments on the Q (since this answer was posted): how many weeks must one wait between weekends with full moons? – John Bollinger Sep 11 '22 at 15:48
  • 4
    @Mark yes, the length of the lunar month doesn't matter over a long period of time. The concept you want is Ergodicity. Over a short period of time it's false (e.g. the answer to "if it is a full moon this weekend, what is the probability that it will be a full moon next weekend?" is zero), but averaged over a longer period of time, every moon phase occurs on every day of the week with equal probability. – hobbs Sep 11 '22 at 16:15
  • @hobbs A comment under my new Math SE question linked above points to https://en.wikipedia.org/wiki/Equidistribution_theorem Now I have to figure out (or better yet, ask about) how the two concepts overlap. Are all Ergodic systems subject to the equidistribution system? Are all system to which the equidistribution theorm applies necessarily ergotic? I learned a new word today, yay! (ergotic) – uhoh Sep 11 '22 at 22:32
  • 3
    @uhoh Are you actually asking for a source that 2/7 of all days are weekends? Or a source that says that the lunar cycle is not synchronised to calendar weeks? (For example, if a the lunar cycle were EXACTLY 4 calendar weeks, then either ALL full moons would be at the weekend, or NONE of them would). – Dawood ibn Kareem Sep 11 '22 at 22:46
  • @DawoodibnKareem no, that's a mischaracterization via oversimplification – uhoh Sep 11 '22 at 22:49
  • 4
    So which part of the answer do you think needs additional sourcing? – Dawood ibn Kareem Sep 11 '22 at 23:06
  • BTW, that Fred Espenak link I posted earlier is from his six millennium catalog of Moon phases, if someone wants to write a scraper and do some stats... – PM 2Ring Sep 12 '22 at 00:50
  • @DawoodibnKareem you didn't @ me but I think your comment is directed at me. Motion of the Sun-Earth-Moon system is not a perfect random number generator. It's a complex system so those of us who care rather than wave our hands give it some thought. See the links in my previous comments; there's a nice body of mathematical work on this topic. JamesK frequently writes completely unsourced answers which is antithetical to "good Stack Exchange answer" writing. At least a reference to ergoticity and/or a link to the equidistribution theorem in Wikipedia would be fine. – uhoh Sep 12 '22 at 21:09
  • @DawoodibnKareem I understand that most folks are fine with "It's just common sense" but we shouldn't just target the lowest common denominator when writing Stack Exchange answers. – uhoh Sep 12 '22 at 21:12
7

Some further info on the actual distribution pattern.

The synodic month and the week length is descended by 1.53059 days, so one month later the full moon comes 1.53059 days later in the week.

That means here are two types of full moon weekends. The first type is where the full moon hits the weekend, but one month later, 1.53059 days is enough to bring it past midnight Sunday. The isolated full moon weekend.

In the other type, the full moon falls early enough in the weekend that 1.53059 days is still Sunday, meaning there will be a full moon weekend pair 4 weeks apart.

The same applies to the wait for the 1.53059 days to work itself through the 5 weekdays. This is has to be exactly 12 or 16 weekends in a row without a full moon.

Full moon weekend pairs have some constraints though. The earliest in the weekend the second full moon of the pair can fall is Sunday afternoon, so the next full Moon can be on a Tuesday on the earliest.
full moon weekend pairs are followed and preceded by the short waiting period of 12 weekends without a full moon.

Pattern:

  • 12 weekends without a full moon
  • Full moon weekend!
  • 3 weekends without a full moon
  • Full moon weekend!
  • 12 weekends without a full moon
  • 1 to 4 repetitions of an isolated full moon weekend, interspaced by either the 12 weekend or 16 weekend waiting period
  • goto 1

full moon weekend

Toby Speight
  • 495
  • 3
  • 11
SE - stop firing the good guys
  • 4,655
  • 20
  • 38
4

Assuming the average properties of the moon's orbit apply out to infinity, we could easily assume the answer is 2/7. But, over any finite period of time, a perfectly even distribution would be highly unlikely.

The below Python code uses PyEphem to find each full moon. I choose to start from 1600 to avoid any confusion over the change to the Gregorian calendar, and then go about just as far forward as I did backwards to 2800.

Results: Total Full Moons: 14841

DOW       #    %
Monday    2116 14.25779934
Tuesday   2123 14.30496597
Wednesday 2122 14.29822788
Thursday  2117 14.26453743
Friday    2125 14.31844215
Saturday  2115 14.25106125
Sunday    2123 14.30496597

Weekend   4238 28.55602722

A perfectly even distribution would have resulted in 28.5714% weekend full moons.

The code (on most platforms "pip install pyephem" will install the ephem dependency).

#!/usr/bin/python
import ephem
from datetime import datetime

days=[0,0,0,0,0,0,0]
count=0
fm = ephem.next_full_moon('1600/1/1')
d=datetime.strptime(str(fm),"%Y/%m/%d %H:%M:%S")


while d.year<2800:
    days[d.weekday()]+=1


fm = ephem.next_full_moon(fm)
d=datetime.strptime(str(fm),&quot;%Y/%m/%d %H:%M:%S&quot;)
count+=1




print(count)
print(days)
Greg Miller
  • 5,857
  • 1
  • 14
  • 31
  • Well, certainly 4,238 of anything can't be distributed evenly into 7 buckets :) – hobbs Sep 12 '22 at 21:06
  • 1
    @hobbs The total number of samples is 14841, not 4238; although your point still stands, since that is also not divisible by 7. However, it's still clear that the distribution isn't quite even; the "perfect" distribution would be six days with 2120 full moons, and one with 2121 (2120 * 7 + 1 = 14841). Using percentages just makes things more confusing, since 100 isn't divisible by 7. – IMSoP Sep 13 '22 at 10:45
  • @hobbs, not sure what you're getting at. The fact that an arbitrary finite interval has about a 1/7 chance of being impossible to distribute evenly just re-emphasizes my point. – Greg Miller Sep 13 '22 at 13:39
  • You probably need to tell us which time zone you used for your calculations, as that certainly affects the distribution (because the time zone determines when midnight occurs). – Toby Speight Jan 26 '23 at 07:22