4

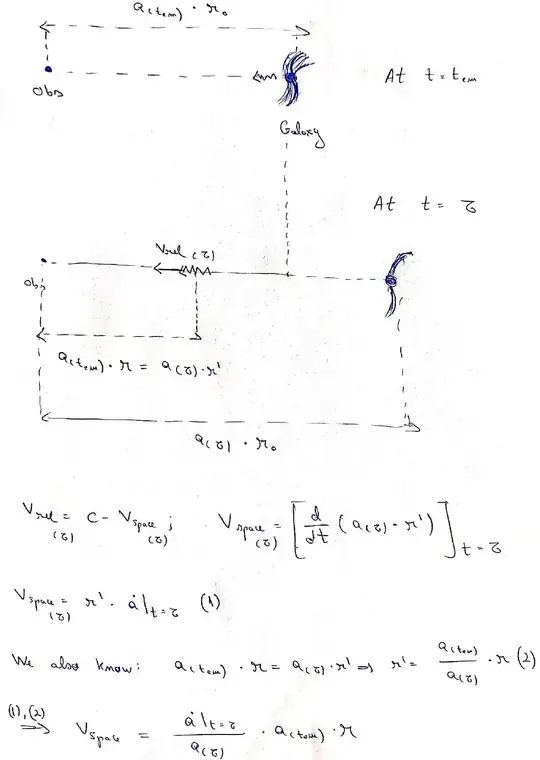
So I tried deriving the radial co-moving coordinate formula to an observable galaxy for which the light observed at time $t_o$ was emitted at time $t_{em}$. i.e $r_0=\int_{t_{em}}^{to} c/a_{(t)} dt$

I tried deriving it without thinking about the Robertson-Walker metric, but with the relative velocity of light in space (the photon being like a boat on a water stream)

I think I might've made a conceptual error, and I hope that by posting my solution here someone will enlighten me.

enter image description here

enter image description here

In the above pictures $\tau$ is a chosen time with the property $t_o > \tau > t_{em}$; $v_{space}$ is the velocity of "space" (universe expansion) at the location of the photon (as you might've noticed, the relative velocity of the photon is given by the speed of light minus the speed of space); $r'$ is the "current" co-moving coordinate (at time $\tau$) while $r$ is the "old" (at emission) co-moving coordinate of the photon.

I'm sorry in advance if something is unclear. Feel free to ask for more clarification.

uhoh
  • 31,151
  • 9
  • 89
  • 293
CosminA
  • 63
  • 2

1 Answers1

1

You can derive the comoving distance formula without the Robertson-Walker metric, but not using "the photon being like a boat on a water stream". You need to use that the speed of light is constant as peculiar velocity of the photon.

So let $R(t) = a(t) \, r(t)$ be the proper distance. The rate of change is $$\begin{aligned}R'(t) &= a'(t) \, r(t) + a(t) \, r'(t) \\ &= v_{\rm rec} + v_{\rm pec}\end{aligned}$$ where $v_{\rm rec} = a'(r) \, r(t)$ is the recession velocity, and $v_{\rm pec} = a(t) \, r'(t) = \pm c$ is the peculiar velocity. The formula follows.