How to calculate the shadow on earth of a large orbital disk (low orbit)?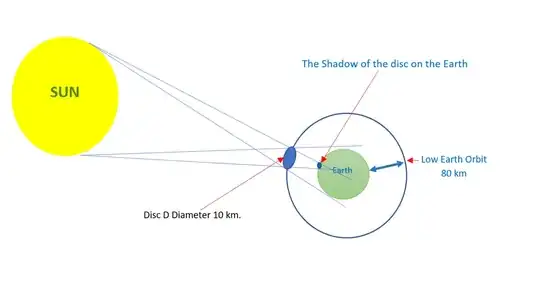
-
For someone who wishes to explain the mathematics, I've done the approximate calculations for half of the problem: the umbra on the Earth's surface should be ~9.25 km in diameter, assuming the curvature of the Earth is negligible (which is an assumption I really shouldn't be making.) – Cloudy7 Oct 03 '19 at 04:43
3 Answers
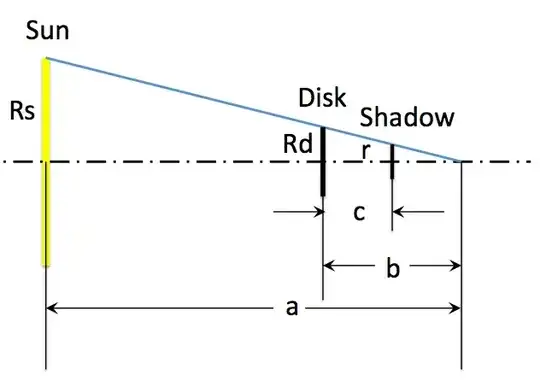
It might be easier to use similar triangles.
$$\frac{Rd}{b} = \frac{Rs}{a}$$
$Rs$ is 696,000 km and $Rd$ is 5 km. $a$ is about 150,000,000 km and c is 80 km.
The the smallest triangle is used next:
$$\frac{r}{b-c} = \frac{Rs}{a}$$
Solve for r and you get
$$r = Rd - Rs \frac{c}{a} = \text{4.63 km}.$$
Extra digits are not helpful because the exact diameter of the Sun depends on how you define it and the distance from the Sun to the Earth varies by almost +/-2 percent.
$Rs/a$ is about 0.00464 and that's also the half-angle of the Sun in radians. Convert it to degrees my multiplying by 180/pi and you get 0.266 degrees, or a quarter of a degree. The full diameter of the Sun is double that, or about a half degree.
- 31,151
- 9
- 89
- 293
-
This is linear optics, which should be fine. It would be interesting to calculate the Spot of Arago for various $R_d$ . – Carl Witthoft Oct 03 '19 at 17:22
-
I considered this, but it doesn't generalize quite as nicely. The one that breaks down first is that c is not going to stay at 80km for larger discs. It also doesn't work close to the Sun, but for this specific case this is indeed all you need. – SE - stop firing the good guys Oct 03 '19 at 17:28
-
A priori, you cannot know that $a$ is about 150 million km - for example, what if the disk had the same diameter as the Sun? Instead, $(R_d-r) : (R_s-R_d) = c : (a-b)$ and $a-b$ is the distance from Sun to disk (so that is approximately 150 million km) – Hagen von Eitzen Oct 03 '19 at 18:34
-
Thank you very much for your reply. Your information was very useful to me. They confirmed my hypothesis.
Do you think an orbit of less than 80 km could be used to place such a disk? What could be the lowest orbit, in your opinion, low altitude circular view, on which such a disk could be placed?
– Ion Corbu Oct 03 '19 at 20:29 -
To keep such a disk in orbit would be two solutions:
- The disk has an orbital speed of about 21,000 km / hour. That is, it rotates around the Earth in about 90 minutes. Possible solution but that does not interest me.
-
- To have propellants (thermochemical, electrical, electromagnetic, ionic. Photonic) that would be the force required to keep such a disk in orbit (80 km) above a fixed point. To counteract gravitational force. And to prevent the disc from falling into orbit and its disintegration. The specific weight of such a disc could be about 10kg / m2
– Ion Corbu Oct 03 '19 at 20:30 -
1That's a different question, but things at 80 km will not stay in orbit very long due to atmospheric drag. If you'd like to explore that, please ask a separate question. – uhoh Oct 04 '19 at 01:40
Playing around with a computer algebra system, the problem actually has an exact solution, but it is ugly enough that a much more simple numerical approximation is more practical.
First, we need to find the angle of the shadow cone peak.
The peak, the centre of the Sun, and the tangent point on the Sun form a triangle with a right angle. Therefore, half the peak angle can be expressed as:
$$v = \sin^{-1}\left(\frac{r_{sun}}{r_{peak}}\right)$$
We don't have $r_{peak}$, but we have the distance from the Sun to the Earth, which is very close. This can give us a first estimate for the angle.
To correct the angle, we can calculate a new $r_{peak}$:
$$r_{peak} = r_{earth-orbit} - r_{LEO} + \frac{r_{disk}}{\tan(v)}$$
Using the new $r_{peak}$ to calculate a new $v$ should converge very quickly to the new angle.
I get $v = 0.004651$
Now, we need to find how this shadow cone projects on the Earth.
To calculate the radius of the projected disk, which has its centre slightly below the surface, we simply have to scale the disk by the cone steepness and distance between the disk, $d$.
$$r_{umbra} = r_{disk} - d\tan(v)$$
Again, we don't exactly have $d$, but the orbital altitude is very close. But we can use the $r_{umbra}$ estimate we obtained to get a better $d$:
$$d = r_{LEO} - \sqrt{r_{earth}^2 - r_{umbra}^2}$$
And yet again, the values should converge very quickly.
I get $r_{umbra} = 4.628 km$
To get the radius on the curve of the Earth instead, you can calculate the central angle and multiply with the circumference of the earth, but at 4 significant figures, the result is still $4.628 km$
- 4,655
- 20
- 38
-
2This appears to assume that the Sun and the disk are directly overhead. When this is not true, which will be most of the time, the shadow will be something more like an ellipse, but, because the shadow will be further from the disk, the region of full shadow may be smaller or non-existent. – Steve Linton Oct 03 '19 at 09:53
-
1It does indeed assume that, as that's what the OP appears to assume in their diagram. – SE - stop firing the good guys Oct 03 '19 at 10:13
-
Thank you very much for your reply. Your information was very useful to me. They confirmed my hypothesis.
Do you think an orbit of less than 80 km could be used to place such a disk? What could be the lowest orbit, in your opinion, low altitude circular view, on which such a disk could be placed?
– Ion Corbu Oct 03 '19 at 20:28 -
To keep such a disk in orbit would be two solutions:
- The disk has an orbital speed of about 21,000 km / hour. That is, it rotates around the Earth in about 90 minutes. Possible solution but that does not interest me.
-
- To have propellants (thermochemical, electrical, electromagnetic, ionic. Photonic) that would be the force required to keep such a disk in orbit (80 km) above a fixed point. To counteract gravitational force. And to prevent the disc from falling into orbit and its disintegration. The specific weight of such a disc could be about 10kg / m2
– Ion Corbu Oct 03 '19 at 20:29
Let's see how far we get without a calculator (so possibly only approximately).
Approximating the Sun as a point source and infinitely far away and the ground as flat, the shadow of the disk is a sharp disk of diameter $10\,\text{km}$. But the Sun is not a point source. From the top of our head, we may recall that the Sun (and the Moon) have an angular diameter of about half a degree. Converted to radians: $\frac12^\circ\cdot\frac\pi{180^\circ}\approx 0.009$. Multiply with the $80\,\text{km}$ altitude to arrive at $\approx 700\,\text{m}$ as the thickness of the penumbra annulus, which has the original disk boundary in its middle, i.e., the central shadow is $\approx 10\,\text{km}-700\,\text{m}$ wide and the penumbra to its outer edge is $\approx 10\,\text{km}+700\,\text{m}$ wide.
- 149
- 5