Canvas and bowling ball

Question

I'm having trouble understanding the basic model for how matter bends space. The classic illustration is the canvas and the ball but that model needs a reference frame where one can define a downward direction to work. For the life of me I can't figure out why matter just doesn't "sit" in space. I'm sorry this question isn't better formulated, maybe someone can point me towards a video or something?

Answer 1

I'm having trouble understanding the basic model for how matter bends space.

No wonder, because it doesn't. It curves spacetime. But spacetime isn't the same thing as space. See this Baez article: "Similarly, in general relativity gravity is not really a 'force', but just a manifestation of the curvature of spacetime. Note: not the curvature of space, but of spacetime. The distinction is crucial". Space isn't curved where a gravitational field is. Instead spacetime is.

The classic illustration is the canvas and the ball but that model needs a reference frame where one can define a downward direction to work.

That's right, it uses gravity to "explain" gravity, so it isn't ideal. However there is a way to understand it, and IMHO it's simpler than you think.

For the life of me I can't figure out why matter just doesn't "sit" in space.

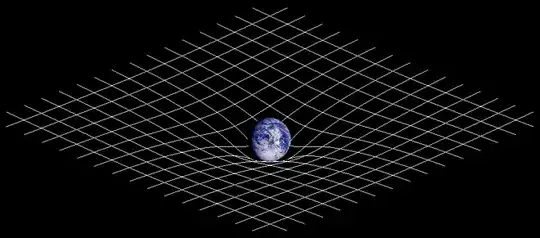
It does just sit in space. And it causes gravity because it's a concentration of energy that "conditions" the surrounding space. It alters it, and this alteration diminishes with distance. Remember the stress-energy tensor, remember that stress is directional pressure, and think of matter as exerting an outward pressure in all directions in the surrounding space. Something like this:

_{Earth image courtesy of NASA, lines drawn by me}

Then see the Einstein digital papers, where Einstein said a gravitational field is a place where "space is neither homogeneous nor isotropic". This inhomogeneity isn't linear. You can plot it, using say optical clocks dotted throughout an equatorial slice through the Earth and the surrounding space. You plot lower slower clocks as lower down in a 3D image, and higher faster clock rates higher up. When you've finished your plot looks like this:

_{CCASA image by Johnstone, see Wikipedia}

The upper image is a bit like looking at the lower image from underneath. But anyway, your plot is curved, and you made it using clocks in space, so we can say spacetime is curved. Note that whilst we started with a two-dimensional equatorial slice and ended up with a three-dimensional curved plot, there is no extra dimension in any real sense. All we're depicting is the "coordinate" speed of light. This might sound unfamiliar but again see the Einstein digital papers: "the curvature of light rays occurs only in spaces where the speed of light is spatially variable". Light doesn't curve because your plot of optical clock rates is curved. It doesn't curve because spacetime is curved. Einstein never actually said that. He said it curves because the speed of light varies. Hence the tilted light-cones on John Norton's course. Light curves wherever your plot isn't flat. Where the speed of light varies. It's actually rather like sonar:

_{Image courtesy of FAS and the US Navy, see course ES310 chapter 20}

Answer 2

I don't think this should be voted down. It's a perfectly fine question to ask about trying to understand a concept.

In one sense, the two dimensional surface stretching downward into a 3rd dimension can be entirely replicated, but impossible to draw with 3 dimensions stretching down into a 4th dimension.

We can only see 3 dimensions so visualizing a 4th dimension is very difficult for most of us, but mathematically it's relatively simple to do.

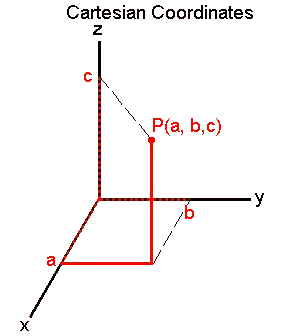
Instead of 3 coordinates (X,Y and Z), (a 3d Cartesian coordinate system), you have 4 coordinates, (X,Y,Z and W). Where a 3 dimensional "rubber sheet", X,Y,Z stretches it into W space, similar to how the 2d rubber sheet X,Y stretches into into Z.

Another example of 2 d space in 3 dimensions is the surface of a sphere. The surface of the Earth can be measured by 2 coordinates, Longitude and Latitude, but it obviously stretches around 3 dimensions.

"Where does space stretch into", well, the rubber sheet analogy isn't perfect. It's more accurate (I think) to think of the depressions in the rubber sheet as gravitational wells, where objects speed up as they approach and slow down as they fly away, they also change direction and in the case of light, which can't speed up or slow down, it blue shifts going in, red shifts coming out, and it's affected by time dilation. Changing properties of space and gravitational force towards are perhaps more accurate ways to think about it than stretched space (in my non-expert opinion).

But does space stretch at all? Yes, it does. The radius becomes longer than it should around massive objects. This article explains the effect with our sun. It's small.

From the article:

The Euclidean result tells us that for each mile we come closer to the sun, the circumference of the circle is diminished by 2π miles.

Because of the presence of the sun, space around the sun is not exactly Euclidean. According to general relativity, for each mile that we come closer to the sun, the circle does not lose 2π miles in circumference; it loses only (0.99999999)x2π miles.

If someone here wants to explain this in more physical terms in their own words, please feel free. I'm a little bit over my head, but the article above explains some of the misleading aspects of the rubber sheet analogy.