Why most planets don't spin retrograde?

Question

Edit: just found duplicate

Since orbital velocity is greater on small orbits, and smaller on large orbits, why don't planets spin retrograde around their own axis?

One portion of planet's mass is closer to its star, and should move prograde relative to center of mass.

Part of the planet's mass far from the star orbits higher and should move retrograde relative to center of mass,

which should create a resulting retrograde spin, with rotation speed depending on planet's diameter.

What's wrong with this? ( since fact is : most planets spin prograde )

In this not to scale second illustration, planet is replaced by two masses linked by a beam. Kepler's law of equal surfaces swept per unit of time is used to display the retrograde rotational force that should be applied relative to center of mass, which orbits black path.

EDIT : Ok I think I found where my mistake is(?) Differential gravitational pull (yellow arrows) counteracts retrograde rotational force (green arrow) Which results in no rotational force at all. Anyway I still don't get how conservation of momentum of everything orbiting the sun, also applies to spin direction of orbiting objects.

Answer 1

Basically, go back to the pre-planet particle clouds, and as explained in

geek.com,

To answer the question we have to go back to the beginning, to the formation of a solar system like ours. Before a star and its planets exist, there’s just a cloud of disorganized gas and small molecules. This is often called a molecular cloud or “stellar nursery.” The Eagle and Orion Nebulae are some of the more famous stellar nurseries we have been able to observe with the Hubble Space Telescope. These clouds are composed mostly of molecular hydrogen, which wouldn’t be able to congregate outside the dense molecular clouds. These clouds can be of any size — not just massive structures like the Orion Nebula. Over time the energy of the molecules in the cloud pushing outward can be overcome by slower molecules collapsing together farther in. As long as there is sufficient mass in the molecular cloud, it continues collapsing in toward the center until it reaches a high enough mass to fuse hydrogen and become a new star. The spin that we see quite clearly now is related to the process of the molecular cloud collapsing. The original cloud was very, very large and made up of many individual molecules and small clumps of matter. On that scale, there is some small amount of rotation within the cloud. It could be caused by the gravity of nearby stellar objects, local differences in mass as the cloud churns, or even the impact of a distant supernova. The point is, most molecular clouds have at least a little rotation.

As the cloud collapses to form a star, it has what physicists call angular momentum. This is the movement an object has as it rotates around a central point. In a large system like a molecular cloud, each particle has some angular momentum, and it all adds together across a very wide area. That’s a lot of momentum, and it is conserved as the cloud continues to collapse. But how does that get us to objects that spin and orbit?

Imagine a figure skater spinning around with arms outstretched. That is a model of angular momentum just like a collapsing cloud of gas. When the arms are drawn inward, the rotational velocity goes up because the total angular momentum is conserved unless there is some external force acting on it. There are such forces acting on the figure skater, but less so on a collapsing molecular cloud. So if a molecular cloud was maybe a light year across, then collapsed down to be just a fraction of that, it would be a huge change in size. Just like the figure skater pulling her arms in, the velocity must increase to conserve angular momentum and therefore form a spinning protostellar disc. It is from this orbiting matter that all the planets form, and of course, they are also spinning and orbiting in the same direction because of the conservation of angular momentum.

Quoting from wikipedia as to the mystery of the misbehaving planets:

All eight planets in the Solar System orbit the Sun in the direction that the Sun is rotating, which is counterclockwise when viewed from above the Sun's north pole. Six of the planets also rotate about their axis in this same direction. The exceptions—the planets with retrograde rotation—are Venus and Uranus. Venus's axial tilt is 177 degrees, which means it is spinning almost exactly in the opposite direction to its orbit. Uranus has an axial tilt of 97.77 degrees, so its axis of rotation is approximately parallel with the plane of the Solar System. The reason for Uranus's unusual axial tilt is not known with certainty, but the usual speculation is that during the formation of the Solar System, an Earth-sized protoplanet collided with Uranus, causing the skewed orientation.[6]

It is unlikely that Venus was formed with its present slow retrograde rotation, which takes 243 days. Venus probably began with a fast prograde rotation with a period of several hours much like most of the planets in the solar system. Venus is close enough to the Sun to experience significant gravitational tidal dissipation, and also has a thick enough atmosphere to create thermally driven atmospheric tides that create a retrograde torque.

Answer 2

That is an intersting question as this is far from being obvious. Actually, for quite some time it was believed that planets should indeed spin retrograde (we can at least track it back to Laplace in his Exposition du Système du Monde published in 1976 where he developed his nebular hypothesis).

How to prove that planet should spin prograde? We'll have to go back to their formation history. Let's start with an ideal case: particles moving in eliptical orbits around a central object of mass $M$, with a proto-planet of mass $m_0$, and rotating in a eliptical orbit. Let's look at what happens at a given point at a distance $r$ from the central object. First, for a planetesimal in a tangential external orbit, then for a planetesimal in a tangential internal orbit.

Tangential external orbit

We can write Newton's Second Law ${\bf F} = m {\bf a}$ and project it on the current trajectory axis (normal and tangent), knowing that the acceleration is always something like $v^2/R$, with $R$ the curvature radius (that is different from $r$, the distance to the central object). We get for the normal component:

$$\frac{GM}{r^2} \cos \alpha = \frac{v_{ext}^2}{R_{ext}^2},$$

$R_{ext}$ being the curvature radius of the planetesimal in an external orbit. For the proto-planet:

$$\frac{GM}{r^2} \cos \alpha = \frac{v^2}{R^2},$$

$\alpha$ having the same value for both object, since it denotes the angle between the direction toward the curvature center and the central object and the orbits being tangential at this specific point, where $r$ the distance to the central object is also the same. Therefore:

$$\frac{v^2}{R^2} = \frac{v_{ext}^2}{R_{ext}^2}.$$

As $R < R_{ext}$, we have $v < v_{ext}$.

Tangetial internal orbit

With the same argument, we can show that $v > v_{int}$ (I let it as an exercice; extra bonus point if you do it with the energy conservation law).

Consequences

If you go in the reference frame of the protoplanet, you will see the internal planetesimal, rotating at a lower speed, coming backward, towards the proto-planet, and the external planetesimal, rotating at a faster speed, coming forward:

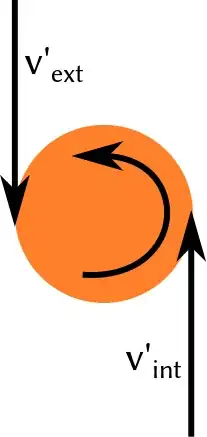
where $v'_{ext}$ and $v'_{int}$ are the velocity of the external and internal planetesimal in the reference fram of the proto-planet. That is why the rotation of the proto-planet tends to be in the same direction as the whole system.