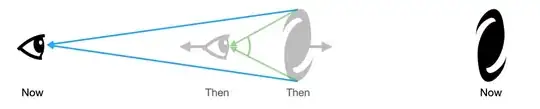
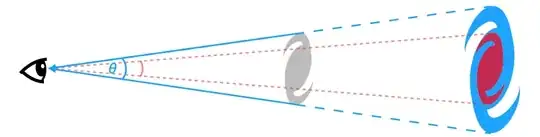
I am trying to get a better understanding of cosmological distances, in particular the angular diameter distance which I have also seen referred to as angular size distance.
What I am looking for is a more detailed explanation of why the angular diameter distance "turns over" in the following graph.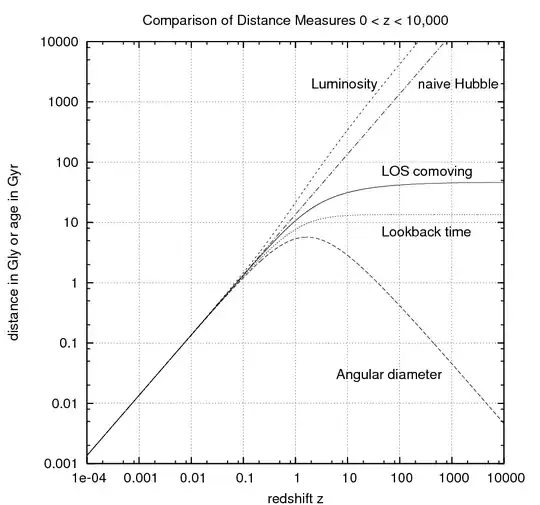
Wikipedia states in their article on angular diameter distance that objects beyond a certain redshift have a smaller angular diameter and as such appear larger on the sky.
I have searched around and have been unable to find a complete explanation of this behaviour and have only found brief answers which state the expansion of the universe or the size of the universe.
I would like if possible for a more detailed explanation as well as the physical significance if any at all of what it means for an object to be at this redshift when they emitted light we are now observing.
Thank you for any feedback or and discussion or suggestions where to look. I would also like to include as it may be of some help that I am currently in my final year of undergraduate studies in physics so please do not hold back any details or technicalities!