I've read that in Mars' poles, the winds can be as fast as 400 km/h, when the poles are exposed to sunlight because the frozen $CO_2$ sublimes. I know that the Martian atmosphere is much thinner than Earth's atmosphere.
So, by knowing the wind speeds on Mars, is there any way to get an idea of its intensity, or in other words, the intensity of a wind of x speed in Mars, to which speed of wind of Earth is comparable, for them to have the same intensity?
Credit to this question for inspiration, though my calculation methods differ.
The dynamic pressure equation is $q=0.5\rho v^2$ where $q$ is the pressure, $\rho$ is the atmospheric density, and $v$ is the wind speed. If we want to know what wind speeds give us equivalent pressures on Earth and Mars, we simply generate dynamic pressure equations for each of them: $q=0.5\rho_e v_e^2$ and $q=0.5\rho_m v_m^2$, set them equal $q=0.5\rho_e v_e^2=0.5\rho_m v_m^2$, and solve for $v_e$ to get $$v_e=\sqrt{\frac{\rho_m}{\rho_e}}v_m$$ where $\rho_m=0.020 \space kg/m^3$ is the atmospheric density for Mars, $\rho_e=1.225 \space kg/m^3$ is the atmospheric density on Earth, $v_m$ is the wind speed on Mars, and $v_e$ is the equivalent wind speed on Earth.
With a velocity ratio of about 7.826 we can plug in a few values for wind speed in kilometers per hour for Mars to get:
v_mars v_earth equivalent
10 1.28
50 6.39
100 12.8
200 25.6
400 51.1
These could be kph, or in fact, any units of velocity. screeenshot
and here's what hat looks like in a plot:
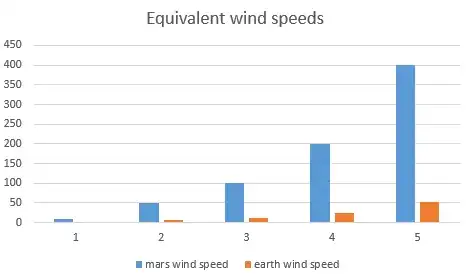
So the 400 kph gust on Mars only has equivalent pressure of a 51 kph gust here on Earth
