Why are the ALMA receivers' ADCs only 3-bits?

Question

above: Table 1 from Performance Highlights of the ALMA Correlators

The ALMA receivers use 3-bit ADCs for what would seem to be to be a high dynamic range application needing much finer quantization to get anything useful.

Then I found these sentences within the abstract of ADC bit number and input power needed, in new radio-astronomical applications:

Abstract- For the most part, so far radio astronomy observations have been performed in protected frequency bands, reserved by ITU for scientific purposes. This means that, ideally, only the amplified equivalent system noise is present at the end of the receiver chain (i.e. the ADC input). So, typically, only a few bits are necessary to describe the signal (VLBI signals are digitised with only 2 bits), but today astronomers, in order to get more sensitivity and to boldly observe where no one has observed before, would like to study the radio sky even outside the protected bands...

And I even found a 1-bit ADC in Performance Measurements of 8-Gsps 1-bit ADCs Developed for Wideband Radio Astronomical Observations.

I think I am just missing something obvious, but I can't understand how a measurement requiring high dynamic range gets by using few-bit ADCs.

edit: Is it possible that the actual conversion of analog to digital is done to a far higher precision than suggested by the number of bits?

Answer 1

It is wasteful to sample with many bits because the signal to noise ratio at the ADC of a radio telescope is typically << 1, so using many bits would just be resolving noise. (An exception to this is when there is strong radio-frequency interference that needs to be resolved, but this is not a big problem for ALMA due to its location and observing frequencies).

High dynamic range measurements arise after averaging together many samples (or correlations of samples), which boosts the SNR to a meaningful level.

Using very few bits at the ADC does introduce quantization noise that reduces the efficiency of the instrument, but 3 bits is enough to achieve 96% efficiency [1].

[1] Convenient formulas for quantization efficiency

Answer 2

The resolution of ADCs is inversely related to their conversion time. Getting more bits requires the signal to travel through more circuitry, which takes time. This is why you can have those high-quality audio ADCs with 18 or 20 bit resolution, which operate at frequencies in kHz range, meaning each conversion can take several milliseconds. At 4GS/s you only have 250 picoseconds at your disposal, so you can only get 3 bits (and only 1 bit at 8GS/s).

how a measurement requiring high dynamic range gets by using few-bit ADCs?

This depends on the nature of the measurement, but the typical solution is to make successive measurements and calculate the average.

Answer 3

Intuitively you think of quantization as something that discards information. That may be true in the end, but it is not a useful way to look at it. Think the other way around, quantization adds an error-signal. If you know what this error signal looks like, it gives you opportunity to analyze how digital processing transforms the error and if it ends up interfering with your desired signal (and how much that interference will be).

ALMA is a phased array, it gets its precision from the correlation of phases if multiple receivers (likewise, phase is typically more important than amplitude in recent modulation schemes). The error function for phase typically is a sawtooth, as the phasor (of a theoretical clean signal) rotates. How the function looks exactly and what the fundamental frequency is, depends on properties of the ADC (and sometimes on AGC settings). The error signal frequency will be n times the received frequency, n=12 or n=8 being typical values. I would have to look into the details of ALMA, I'm not familiar with this one.

Now consider how this error function is sampled. There is no way to attenuate it before sampling, so aliased images of harmonics of this sawtooth end up in your digital data. You can calculate where these harmonics are and how strong they are. And you can shift them by altering the sampling rate (with a given fixed signal frequency). If you want to observe a certain bandwidth and you do optimize sampling rate, you may find that you have f.e. the 11th harmonic (with amplitude 1/11) somewhere in your signal, but you can avoid all the lower (and stronger) harmonics.

Investing in more bits for quantization reduces the amplitude of errors, raising the fundamental freq of the error function at the same time. You may find, that the contribution of quantization errors is already in the magnitude of other noise sources, so there is not much to gain for overall system performance. This is typically the case for direct code spread spectrum applications like GNSS systems.

Answer 4

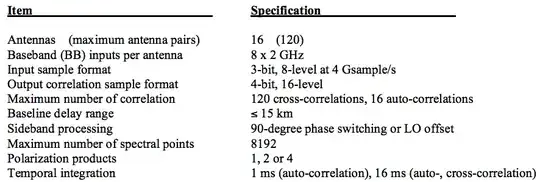
I found an authoritative document stating that the ADC’s are certainly only 3 bits. See the ALMA Technical Handbook, https://almascience.nrao.edu/documents-and-tools/cycle7/alma-technical-handbook/view .

From Chapter 5.6.1:

A digitizer adds quantization noise to its input analog signal, with a consequent signal-to-noise reduction or sensitivity loss. The ALMA digitizer employs 3-bit (8-level) quantization, and additional re-quantization processes are applied in the correlators.

One could ask this question a different way, “What would the benefit be for adding additional bits (beyond 3) to ALMA’s ADCs?” You don’t get much higher sensitivity since the 3-bit ADCs are already ~96% efficient (as noted in Ben Barsdell’s excellent answer). You don’t get better angular resolution, since the angular resolution in interferometry is a function of the signal wavelength, distance to the emission source, and antenna location geometry (further distances between antenna pairs increases angular resolution). On the other hand, you get considerable additional computational load. The one good thing you get from adding bits to your ADC is that you can pick up a fainter signal in the presence of noise that would normally saturate your ADC. Hence the statement made by ALMA that they want to observe in frequency bands that aren’t restricted.

I agree that it’s un-intuitive that 3 bit ADCs are sufficient for such an incredible instrument as ALMA. But remember that Nyquist says you might have more data than you think you do:

A bandlimited continuous-time signal can be sampled and perfectly reconstructed from its samples if the waveform is sampled over twice as fast as it's highest frequency component.

ALMA can sample at Nyquist (for most radio telescopes it is set to 2.1x of the upper end of the observing frequency window) or twice Nyquist frequency. The digitized data is the raw data and doesn’t look like it has any information. But after the digitized data is run through an FFT, you get a spectrogram and there is a wealth of information that was in the raw data. Radio Astronomers almost never look at the raw data. The spectrogram gives them the RF signature and emitted power.

When I observed on the GBT, we were looking for gas clouds of formaldehyde near the center of the milky way. When cosmic formaldehyde gets dense enough, it starts to absorb the CMB. We could see the dips in the spectrogram corresponding to the rf quantum shifts in the molecules. Dense formaldehyde clouds are a sign of early star formation. Fun stuff.

Would reproducing a giant emitting Mona Lisa in space with a matlab radio telescope simulator with a low bit ADC convince you?

ALMA has low dynamic range over a single set of observations. So you can observe and detect faint radio emissions (like phosphine on Venus) with sensitivities in the microJansky range, but when you observe and detect powerful radio emissions (like solar radio flares) ALMA’s sensitivities need to be set in the megaJansky range. https://en.wikipedia.org/wiki/Jansky

An astronomer who is privileged enough to use ALMA has to set the sensitivity of the telescope prior to observing. If they set the sensitivity too high, they will saturate the ADCs and not get any usable data. If they set the sensitivity too low, they won’t detect the signal they are looking for! ALMA provides a calculator to help the astronomers: https://almascience.eso.org/proposing/sensitivity-calculator . Note the astronomer can choose sensitivity units from microJanskys to degrees Kelvin (which is about a megaJansky).

The typical way to change the sensitivity of a radio telescope is through the use of an attenuator https://en.wikipedia.org/wiki/Attenuator_(electronics) . If the signal you are observing is saturating your ADCs, you turn up the attenuator until the whole signal waveform is contained. For solar observations, they built specialized attenuators for ALMA, described here: https://digitalcommons.njit.edu/cgi/viewcontent.cgi?article=1223&context=theses .

Because ALMA has low dynamic range for a specified sensitivity, astronomers observing faint signals need to do so when there are no stronger emitters at the same frequency in the same part of the sky. If ALMA had high dynamic range, when Venus passed in front of the sun, perhaps an astronomer would be able to observe the sun’s radio emissions at the same time as observing phosphine radio emissions from Venus that were 12 orders of magnitude less powerful. For now, however, astronomers observing for phosphine on Venus would be well advised to do so at night when there are no other stars or planets nearby!

Finally to answer the title question, ALMA's ADCs are only 3 bits because ALMA does not require a high dynamic range. Instead, astronomers must correctly configure the telescope sensitivity to observe and detect the signals they are interested in.