In one hand you have the fact that if the initial step-size is a bit too optimistic, decay will at some point lead to a step-size that works
However, there is a much more theoretical reason for it.
Indeed if you consider a non-smooth function, it's necessary sometimes to converge to decay your stepsize...
As an example, consider $f(x) = |x|$, with an initial guess of $x = 2.5$ and a stepsize of $\alpha = 1$
Well, the gradient of such function is $1$ if $x > 0$ and $-1$ if $x < 0$
Now, apply GD: $x = x - \alpha \nabla_x f(x) \rightarrow x = x - \nabla_x f(x)$, and considering that the gradient on $x = 2.5$ is also 1, becomes $x = x - 1$
Therefore, you will start from 2.5, then next time go to 1.5, then again to 0.5, and at that point, you'll jump to -0.5, and from there jump back to 0.5
As you can see, you will never converge to the optimal $x = 0$, except if you decay your stepsize
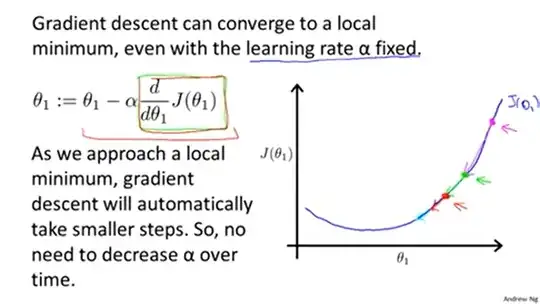 However, there are numerous types of 'learning rate schedules' in TensorFlow that change the learning rate profile as training progresses.
However, there are numerous types of 'learning rate schedules' in TensorFlow that change the learning rate profile as training progresses.