Is the LSTM component a neuron or a layer?

Question

Given the standard illustrative feed-forward neural net model, with the dots as neurons and the lines as neuron-to-neuron connection, what part is the (unfold) LSTM cell (see picture)? Is it a neuron (a dot) or a layer?

Answer 1

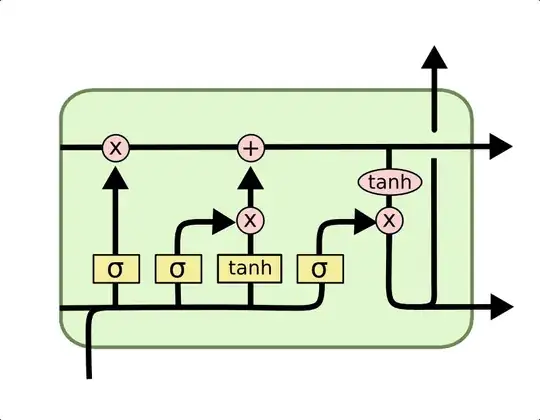
The diagram you show works at least partially for describing both individual neurons and layers of those neurons.

However, the "incoming" data lines on the left represent all inputs under consideration, typically a vector of all inputs to the cell. That includes all data from current time steps (from input layer or earlier LSTM or time-distributed layers) - the line coming up into the LSTM cell - and the full output and cell state vectors from the whole LSTM layer on previous time step - the horizontal lines inside the cell starting on the left. Technically the top left input line could be read as either be a single neuron cell state value, or the full vector of cell state from the previous time step, depending on whether you were viewing the diagram as describing a single neuron in the layer, or the whole layer respectively.

If you visualise this cell connecting to itself over time steps, then the data lines both in and out must be whole layer vectors. The diagram is then best thought of as representing a whole LSTM layer, which is composed of various sub-layers which get combined, such as the forget gate layer (the leftmost yellow box).

Each yellow box in the diagram can be implemented very similar to a single layer of a simple feed forward NN, with its own weights and biases. So the forget gate can be implemented as

$$\mathbf{f}_t = \sigma(\mathbf{W}_f [\mathbf{x}_t , \mathbf{y}_{t-1}] + \mathbf{b}_f)$$

where $\mathbf{W}_f$ is the weight matrix of the forget gate, $\mathbf{b}_f$ is the bias vector, $\mathbf{x}_t$ is layer input on current time step, $\mathbf{y}_{t-1}$ is layer output from previous time step, and the comma $,$ is showing concatenation of those two (column) vectors into one large column vector.

If the input $\mathbf{x}$ is an $n$-dimensional vector, and output $\mathbf{y}$ is an $m$-dimensional vector, then:

• $\mathbf{c}$, the cell state (top line), and all interim layer outputs are $m$-dimensional vectors
• $\mathbf{W}_f$, the forget gate weights, and the three other internal weights matrices are $m \times (n+m)$ matrices
• $\mathbf{b}_f$, the forget gate bias, and the three other internal bias vectors are $m$-dimensional vectors

The other gates are near identical (using their own weights and biases, plus the third cell candidate value uses tanh instead of logistic sigmoid), and have their own weight matrices etc. The whole thing is constructed a lot like four separate feed-forward layers, each receiving identical input, that are then combined using element-wise operations to perform the functions of the LSTM cell. There is nothing stopping you implementing each yellow box as a more sophisticated and deeper NN in its own right, but that seems relatively rare in practice, and it is more common to stack LSTM layers to achieve that kind of depth.