How do I evaluate this integral $\int_0^\pi{\frac{{{x^2}}}{{\sqrt 5-2\cos x}}}\operatorname d\!x$?

Question

Show that $$\int\limits_0^\pi{\frac{{{x^2}}}{{\sqrt 5-2\cos x}}}\operatorname d\!x =\frac{{{\pi^3}}}{{15}}+2\pi \ln^2 \left({\frac{{1+\sqrt 5 }}{2}}\right).$$

I don't have any idea how to start, but maybe I could use the Polylogarithm.

Answer 1

This is a more difficult integral than it appears. Let's define

$$J(a) = \int_{-\pi}^{\pi} dx \frac{e^{i a x}}{\sqrt{5}-2 \cos{x}}$$

Then the integral we seek is

$$-\frac12 J''(0) = \int_0^{\pi} dx \frac{x^2}{\sqrt{5}-2 \cos{x}}$$

To evaluate $J(a)$, consider the following contour integral in the complex plane:

$$\oint_C dz \frac{z^a}{z^2-\sqrt{5} z+1}$$

where $C$ is a "keyhole" unit circle, with the keyhole being about the negative real axis, as pictured below.

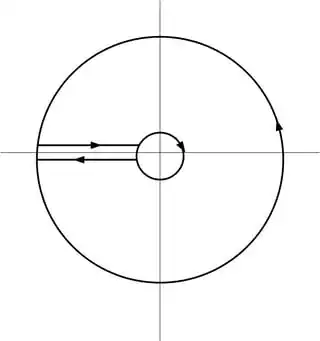
By the residue theorem, this contour integral is equal to

$$-i 2 \pi \phi^a$$

where $\phi = (\sqrt{5}-1)/2$ is the golden ratio. On the other hand, the integral is also equal to

$$-i J(a) + i 2 \sin{\pi a} \, \int_0^1 dx \frac{x^a}{x^2+\sqrt{5} x+1}$$

Note that the portion of the integral that goes about the center goes to zero. Therefore we have

$$J(a) = 2 \pi \phi^a + 2 \sin{\pi a} \, \int_0^1 dx \frac{x^a}{x^2+\sqrt{5} x+1}$$

With some quick work, the integral we seek is then

$$-\frac12 J''(0) = -\pi \log^2{\phi} - 2 \pi \int_0^1 dx \frac{\log{x}}{x^2+\sqrt{5} x+1} $$

Using the fact that

$$\frac{1}{x^2+\sqrt{5} x+1} = \frac{1}{x+\phi}-\frac{1}{x+1/\phi}$$

$$\int_0^1 dx \frac{\log{x}}{x+a} = \text{Li}_2{\left ( -\frac{1}{a}\right)}$$

$$\text{Li}_2{\left ( -\frac{1}{\phi}\right)} = -\frac{\pi^2}{10} - \log^2{\phi}$$

$$\text{Li}_2{\left ( -\phi\right)} = -\frac{\pi^2}{15} +\frac12 \log^2{\phi}$$

We finally have

$$-\frac12 J''(0) = -\pi \log^2{\phi} - 2 \pi \left [\left ( -\frac{\pi^2}{10} - \log^2{\phi} \right ) - \left ( -\frac{\pi^2}{15} +\frac12 \log^2{\phi} \right ) \right ]$$

or

$$ \int_0^{\pi} dx \frac{x^2}{\sqrt{5}-2 \cos{x}} = 2 \pi \log^2{\phi} + \frac{\pi^3}{15}$$

as was to be shown.

Answer 2

Using the identity $$ \sum_{k=0}^{\infty} a^{k} \cos(kx) = \frac{1- a \cos x}{1-2a \cos x + a^{2}} \ \ ( |a| <1) ,$$

one finds that $$ 1 + 2 \sum_{k=1}^{\infty} a^{k} \cos(kx) = \frac{1-a^{2}}{1-2a \cos x +a^{2}}.$$

Therefore

$$ \begin{align} \int_{0}^{\pi} \frac{x^{2}}{1-2a \cos x+a^{2}} \ dx &= \frac{1}{1-a^{2}} \Big( \int_{0}^{\pi} x^{2} \ dx + 2 \int_{0}^{\pi}x^{2} \sum_{k=1}^{\pi} a^{k} \cos (kx) \ dx \Big) \\ &= \frac{1}{1-a^{2}} \Big(\frac{\pi^{3}}{3} + 2 \sum_{k=1}^{\infty} a^{k} \int_{0}^{\pi} x^{2} \cos(kx) \ dx \Big) \\ &=\frac{1}{1-a^{2}} \Big( \frac{\pi^{3}}{3} + 2 \sum_{k=1}^{\infty}a^{k} \frac{2 \pi (-1)^{k}}{k^{2}} \Big) \\ &= \frac{1}{1-a^{2}} \Big( \frac{\pi^{3}}{3} +4 \pi \sum_{k=1}^{\infty}\frac{(-a)^{k}}{k^{2}} \Big) \\ &= \frac{1}{1-a^{2}} \Big(\frac{\pi^{3}}{3} + 4 \pi \ \text{Li}_{2}(-a) \Big) . \end{align}$$

Now express the integral as $$ \frac{1}{1+a^{2}} \int_{0}^{\pi} \frac{x^{2}}{1- \frac{2a}{1+a^{2}} \cos x} \ dx$$

and let $ \displaystyle a = \frac{1}{\varphi}$ where $\varphi$ is the golden ratio.

Then we have$$ \begin{align} \frac{1}{1+\varphi^{-2}} \int_{0}^{\pi} \frac{x^{2}}{1-\frac{2 \varphi^{-1}}{1+\varphi^{-2}} \cos x} \ dx &= \frac{1}{1+\varphi^{-2}} \int_{0}^{\pi} \frac{x^{2}}{1-\frac{2}{\sqrt{5}} \cos x} \ dx \\ &=\frac{\sqrt{5}}{1+\varphi^{-2}} \int_{0}^{\pi} \frac{x^{2}}{\sqrt{5}-2 \cos x} \ dx \\ &= \frac{1}{1-\varphi^{-2}} \Big(\frac{\pi^{3}}{3} + 4 \pi \ \text{Li}_{2} (- \frac{1}{\varphi}) \Big) \\ &= \frac{1}{1-\varphi^{-2}} \Big(\frac{\pi^{3}}{15} + 2 \pi \ln^{2} (\varphi) \Big) \end{align} $$

which implies $$ \begin{align} \int_{0}^{\pi} \frac{x^{2}}{\sqrt{5}-2 \cos x} \ dx &= \frac{1}{\sqrt{5}} \frac{1+\varphi^{-2}}{1- \varphi^{-2}} \Big(\frac{\pi^{3}}{15} + 2 \pi \ln^{2} (\varphi) \Big) \\ & = \frac{1}{\sqrt{5}} \sqrt{5}\Big(\frac{\pi^{3}}{15} + 2 \pi \ln^{2} (\varphi) \Big) \\ &= \frac{\pi^{3}}{15} + 2 \pi \ln^{2} (\varphi) . \end{align} $$

Answer 3

$\newcommand{\+}{^{\dagger}} \newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\down}{\downarrow} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\isdiv}{\,\left.\right\vert\,} \newcommand{\ket}[1]{\left\vert #1\right\rangle} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left( #1 \right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert} \newcommand{\wt}[1]{\widetilde{#1}}$ $\ds{\color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} ={\pi^{3} \over 15} + 2\pi\,\ln^{2}\pars{1 + \sqrt 5 \over 2}:\ {\large ?}}$

$$ \color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} =\half\int_{-\pi}^{\pi}{x^{2} \over 2\varphi - 1 - 2\cos\pars{x}}\,\dd x\tag{1} $$ where $\ds{\varphi \equiv {1 + \root{5} \over 2} \approx 1.6180}$ is the Golden Ratio.

\begin{align} &\color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} =\half \int_{\verts{z}\ =\ 1 \atop {\vphantom{\Huge A}\verts{{\rm Arg}\pars{z}}\ <\ \pi}} {-\ln^{2}\pars{z} \over 2\varphi - 1 -2\,\pars{z^{2} + 1}/\pars{2z}} \,{\dd z \over \ic z} \\[3mm]&=-\,\half\,\ic \int_{\verts{z}\ =\ 1 \atop {\vphantom{\Huge A}\verts{{\rm Arg}\pars{z}}\ <\ \pi}} {\ln^{2}\pars{z} \over z^{2} - \pars{2\varphi - 1}z + 1} \,\dd z\tag{2} \end{align} Zeros $\ds{z_{\pm}}$ of $\ds{z^{2} - \pars{2\varphi - 1}z + 1 = 0}$ are given by: $$ z_{+} = \varphi > 1\,;\qquad\qquad z_{-} = {1 \over \varphi}\,,\quad 0 < z_{-} < 1 $$

Expression $\pars{2}$ is reduced to: \begin{align} &\color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} =-\,\half\,\ic\braces{2\pi\ic\lim_{z \to z_{-}}\bracks{% {\pars{z - z_{-}}\ln^{2}\pars{z} \over z^{2} - \pars{2\varphi - 1}z + 1}}} \\[3mm]&\mbox{}+ \half\,\ic\int_{-1}^{0} {\bracks{\ln\pars{-x} + \ic\pi}^{2} \over x^{2} - \pars{2\varphi - 1}x + 1}\,\dd x + \half\,\ic\int_{0}^{-1} {\bracks{\ln\pars{-x} - \ic\pi}^{2} \over x^{2} - \pars{2\varphi - 1}x + 1}\,\dd x \\[3mm]&=\pi\,{\ln^{2}\pars{1/\varphi} \over 2\pars{1/\varphi} - \pars{2\varphi - 1}} + \half\,\ic\int_{0}^{-1} {-4\pi\ic\ln\pars{-x} \over x^{2} - \pars{2\varphi - 1}x + 1}\,\dd x\tag{3} \end{align}

Since $\ds{2\,{1 \over \varphi} - \pars{2\varphi - 1} = -1}$, expression $\pars{3}$ becomes: \begin{align} &\color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} =-\pi\ln^{2}\pars{\varphi} -2\pi\int_{0}^{1}{\ln\pars{x} \over x^{2} + \pars{2\varphi - 1}x + 1}\,\dd x \tag{4} \end{align} Roots of $\ds{x^{2} + \pars{2\varphi - 1}x + 1 = 0}$ are $\ds{-\varphi}$ and $\ds{-\,{1 \over \varphi}}$ such that $\pars{4}$ is written as:

\begin{align} &\color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} \\[3mm]&=-\pi\ln^{2}\pars{\varphi} - 2\pi\int_{0}^{1}\ln\pars{x}\bracks{% \pars{{1 \over x + \varphi} - {1 \over x + 1/\varphi}}\ \overbrace{\pars{{1 \over \varphi} - \varphi}^{-1}}^{\ds{=\ -1}}}\,\dd x \\[3mm]&=-\pi\ln^{2}\pars{\varphi} + 2\pi\bracks{% \int_{0}^{1}{\ln\pars{x} \over \varphi + x}\,\dd x -\int_{0}^{1}{\ln\pars{x} \over 1/\varphi + x}\,\dd x}\tag{5} \end{align}

With $\ds{a > 0}$: \begin{align} \int_{0}^{1}{\ln\pars{x} \over a + x}\,\dd x&= -\int_{0}^{1}{\ln\pars{-a\bracks{-x/a}} \over 1 - \pars{-x/a}}\, \pars{-\,{\dd x \over a}} =-\int_{0}^{-1/a}{\ln\pars{-ax} \over 1 - x}\,\dd x \\[3mm]&=\left.\vphantom{\LARGE A} \ln\pars{1 - x}\ln\pars{-ax}\,\right\vert_{\,x\ =\ 0}^{\,x\ =\ -1/a} -\int_{0}^{-1/a}\ln\pars{1 - x}\,{-a \over -ax}\,\dd x \\[3mm]&=\int_{0}^{-1/a}{-\ln\pars{1 - x} \over x}\,\dd x =\int_{0}^{-1/a}{{\rm Li}_{1}\pars{x} \over x}\,\dd x\tag{6} \end{align} where $\ds{{\rm Li}_{s}\pars{z}}$ is the Polylogarithm Function which satisfies the recurrence relation $${\rm Li}_{s + 1}\pars{z} = \int_{0}^{z}{{\rm Li}_{s}\pars{t} \over t}\,\dd t\qquad\mbox{and} \qquad -\ln\pars{1 - z} = {\rm Li}_{1}\pars{z} $$ $$ \mbox{Expression}\ \pars{6}\ \mbox{becomes}\quad \begin{array}{|c|}\hline\\ \quad\int_{0}^{1}{\ln\pars{x} \over x + a}\,\dd x ={\rm Li}_{2}\pars{-\,{1 \over a}}\quad \\ \\ \hline \end{array} \,,\qquad\qquad{\rm Li}_{2}\pars{0} = 0 $$ such that $\ds{\pars{~\mbox{see expression}\ \pars{5}~}}$ $$ \int_{0}^{1}{\ln\pars{x} \over x + \varphi}\,\dd x -\int_{0}^{1}{\ln\pars{x} \over x + 1/\varphi}\,\dd x ={\rm Li}_{2}\pars{-\,{1 \over \varphi}} -{\rm Li}_{2}\pars{-\varphi} $$

Expression $\pars{5}$ is reduced to: $$ \color{#c00000}{\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} =-\pi\ln^{2}\pars{\varphi} + 2\pi\bracks{% {\rm Li}_{2}\pars{-\,{1 \over \varphi}} - {\rm Li}_{2}\pars{-\varphi}}\tag{7} $$ With the identities \begin{align}&\left.\begin{array}{rcl} {\rm L_{i}}_{2}\pars{-\,{1 \over \varphi}} & = & -\,{\pi^{2} \over 15} + \half\,\ln^{2}\pars{\varphi} \\[1mm] {\rm L_{i}}_{2}\pars{-\varphi} & = & -\,{\pi^{2} \over 10} - \ln^{2}\pars{\varphi} \\[5mm] \mbox{we find}\quad {\rm Li}_{2}\pars{-\,{1 \over \varphi}} - {\rm Li}_{2}\pars{-\varphi} & = & {\pi^{2} \over 30} + {3 \over 2}\,\ln^{2}\pars{\varphi} \end{array}\right\rbrace \end{align}

the final result is given by: $$ \color{#00f}{\large\int_{0}^{\pi}{x^{2} \over \sqrt 5 - 2\cos\pars{x}}\,\dd x} ={\pi^{3} \over 15} + 2\pi^{2}\ln\pars{\varphi} =\color{#00f}{\large{\pi^{3} \over 15} + 2\pi\ln^{2}\pars{\root{5} + 1 \over 2}} $$