6

I need to calculate volume of irregular solid which is having fix $200 \times 200$ width and breadth but all four points varies in depth.

Illustration

I have table which gives depth at each point.

How to calculate volume of such solid?

Hi, I am giving here my main problem definition. I have a grid with size $200 \times 200$ and the depth at each point is given in array. For $2 \times 4$ grid, below is the depth level.

And i need to find volume of such solid.

537.52, 707.52, 742.52, 719.52, 654.52

631.52, 783.52, 795.52, 764.52, 727.52

597.52, 868.52, 846.52, 793.52, 707.52

In Image i have tried to plot first grid cell.

Any help/pointer/suggestion would be real help.

I found some post related to this. But not sure which will give best result. http://tutorial.math.lamar.edu/Classes/CalcI/MoreVolume.aspx (Example 2) and link 2 answers.yahoo.com/question/index?qid=20080804220134AA8skGw

Please comment your views. Thanks a lot in advance.

user1211476
  • 71
  • I don't understand how your solid is described. Is your solid a polyhedron, i.e. bounded ba finitely many palnar faces between finitely many vertices? – Hagen von Eitzen Jul 08 '13 at 12:11
  • Do your solid has a rectangular base and 4 "vertical" sides? If not, a picture would help a lot to clarify what sort of solid you are dealing with. – achille hui Jul 08 '13 at 12:17
  • Hi, you can say it is about finding volume of rock. and it has fixed width and breadth but variable height. I wanted to post a picture but because of "low reputation" in forum, I could not. just assume it as base square with different height. – user1211476 Jul 08 '13 at 12:54
  • 1
    Is the "top" supposed to be a single flat (but tilted) quadrilateral? (The figure would be a truncated right-rectangular prism.) If so, then the "depths" to opposite corners of the base must add-up to the same value. This does not happen with your sample points: $30 + 80 \neq 0 + 120$. If you're allowing that the "top" might be sub-divided into triangles, then you really want the formula for the volume of a truncated right-triangular prism. – Blue Jul 08 '13 at 13:25
  • Hi, the irregular shape i am talking about can be something like this. http://imgur.com/nS322jz – user1211476 Jul 08 '13 at 14:24
  • What the other answers suggest is equivalent to the 2-d version of Trapezoidal rule in computing an integral. If the heights of the top surface is available in the form of a rectangular grid, you can also try the 2-d version of Simpson's rule. Some details can be found here. Personally, I will calculate the rock's volume using both methods and use the difference of the two calculated volumes as an error estimate. – achille hui Jul 11 '13 at 09:45

3 Answers3

5

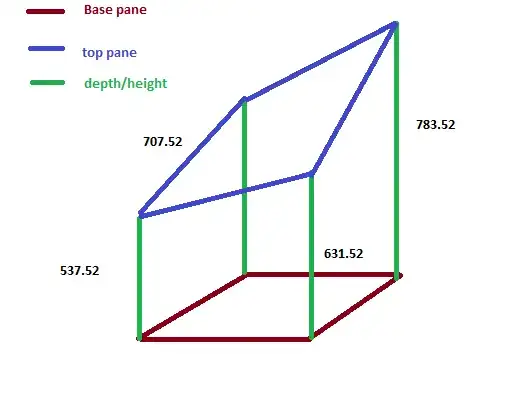
The question statement suggests that OP wants the formula for the volume of a truncated right-rectangular (actually -square) prism; however, the sample data doesn't fit this situation. ("Depths" to opposite vertices must sum to the same value, but $30+80 \neq 0 + 120$.) If we allow the table-top to have one or more creases, then OP can subdivide the square prism into triangular ones and use the formula

$$V = \frac{1}{3} A\;(a+b+c)$$

where $A$ is the volume of the triangular base, and $a$, $b$, $c$ are depths to each vertex of the base.

If the table-top really is supposed to be flat ...

Let the base $\square ABCD$ have edge length $s$, and let the depths to the vertices be $a$, $b$, $c$, $d$; let $h$ be the common sum of opposite depths: $h := a+c=b+d$. Then,

$$V = \frac{1}{2} s^2h$$

This follows from the triangular formula, but also from the fact that you can fit such a prism together with its mirror image to make a complete (non-truncated) right prism with parallel square bases. The volume of that figure $s^2h$ is twice as big as we want, because the figure contains two copies of our target.

Edit. OP comments below that the top isn't necessarily flat, and notes elsewhere that only an approximation is expected. So, let's explore the subdivided prism scenario:

As above, our base $\square ABCD$ has side $s$, and the depths to the vertices are $a$, $b$, $c$, $d$. Let $V_A$ be the volume of the truncated triangular prism over right-triangular base $\triangle BCD$; likewise, $V_B$, $V_C$, $V_D$. Then, by the triangular prism volume formula above ...

$$ V_A = \frac{1}{3} \cdot \frac{1}{2} s^2 \cdot \left(b+c+d\right) = \frac{1}{6} s^2 \left(b+c+d \right) $$ $$ V_B = \frac{1}{6} s^2 \left(a+c+d \right) \qquad V_C = \frac{1}{6} s^2 \left(a+b+d \right) \qquad V_D = \frac{1}{6} s^2 \left(a+b+c \right) $$

Now, $V_A+V_C$ is the volume of the figure where we assume the top is formed by two triangles that meet at a "crease" above diagonal $BD$; and $V_B+V_D$ is the volume when the crease appears above diagonal $AC$. (Note that one of the creases will be a "valley", and one a "ridge".) The desired volume is perhaps somewhere in between, so why not take an average?

$$V = \frac{1}{2}\left( \; (V_A+V_C) + (V_B+V_D) \; \right) = \frac{1}{12}s^2 \left( 3a+3b+3c+3d \right) = \frac{1}{4}s^2 \left( a+b+c+d \right)$$

By the way, we can get the same approximation this way: introduce a new point above the square's center, with a depth equal to the average of the depths at the vertices. Connecting that new point to the vertices creates a "fan" of triangles that approximate the top surface, and each of these triangles hovers over a quarter-square triangular base. The sum of the four triangular solids is the same as our final $V$ above.

Blue
  • 75,673
  • No, my object is not truncated rectangular. It has square base but varies in height. Something like shown in this picturr http://imgur.com/nS322jz. If you can give any suggestion on how to calculate volume of such object, it will be highly appreciable. – user1211476 Jul 08 '13 at 15:55
  • @user1211476: That's a truncated right-rectangular prism. The slanted plane is doing the "truncating". – Blue Jul 08 '13 at 16:56
  • sorry but my solid has different height at each base polygon point. and depths to opposite vertices may not be always equal to sum to the same value. I have added more description to problem. I hope it will clear my problem and get some hint. Many thanks. – user1211476 Jul 09 '13 at 10:10
  • Thank you very much for the suggestion. as mentioned it gives approximate volume. Is it the best/optimum way to calculate volume? I am not maths/geometric expert, so just want to confirm. Is there any other way which will give more approximate(almost realistic) result. May be using calculus? as given in this link. http://tutorial.math.lamar.edu/Classes/CalcI/MoreVolume.aspx (Example 2) or formula given in this link http://answers.yahoo.com/question/index?qid=20080804220134AA8skGw. I am sorry,Im confused. and not having clear vision. Help! – user1211476 Jul 11 '13 at 09:12
  • @user1211476: Since you're approximating your solid with planes, the formula I've given is essentially the approximation for its volume. The result can't get better without more information about, say, how non-planar the surface is ... but, even then, if your terrain is fairly natural, there'll be no perfect way to describe it. If/when you're dealing with bumpier areas of ground, the appropriate strategy would be to use smaller grid sizes, so that within each grid the terrain is reasonably tame. – Blue Jul 11 '13 at 14:35
  • @user1211476: "Calculus" won't improve matters, but what you're doing is called numerical integration. (Look it up!) When, say, we want the area under a curve, we can slice the area into vertical strips, compute the area of each strip from its "depth" and width, and add up those areas. Our strips could be rectangles, with flat tops, but "better" would be trapezoids, with slanted tops that follow the bumpiness of the curve better. (Thin-enough strips make rectangles work fine, provided "thin enough" tames the bumpiness per strip.) The volume formula above amounts to the trapezoid formula in 3D. – Blue Jul 11 '13 at 14:49
2

This is a complete rewrite, for previous versions see the edit history.

From your various comments, I understand that your solid is defined by eight corners, that five sides will be flat but the top side may not, and that you are looking for an approximate solution without worrying too much about the exact shape to the top face.

One viable solution for you might be the following: if the base is a square of edge length $s$, and your heights are $h_1$ through $h_4$, then you can compute the volume as

$$V\approx s^2\frac{h_1+h_2+h_3+h_4}{4}$$

This formula will give you an exact result for the case where the top side is planar. If it is not planar, then this is probably still the best you can get without further information about the actual shape of your top surface.

MvG
  • 42,596
  • Hi MvG, thankyou very much for reply. But it is not tetrahedron. you can assume like it like a cube with different height. so it has square base and all other 5 side is a trapezoid. and if one of the height is 0 then 3 trapezoid and 2 triangle. I hope I am clear with requirement. Thanks again in advance. – user1211476 Jul 08 '13 at 13:07
  • @user1211476: Your description is incomplete. The diagonals between your four corners to not meet in a single point. So the top face cannot be flat. If you want to split it into two triangles, you have two possible ways of doing so, one along each diagonal. By the way, the volume computed above corresponds to the difference between these two solutions. The fact that it its non-zero indicates that the four points are not coplanar. – MvG Jul 08 '13 at 13:15
  • As I could not post pictures here, I have sent a mail. Hope with picture it is helpful to understand problem. – user1211476 Jul 08 '13 at 13:50
  • Hi, the polygon I am talking about can be something like this. http://imgur.com/nS322jz – user1211476 Jul 08 '13 at 14:22
  • Am i clear with my requirements now? – user1211476 Jul 08 '13 at 15:33
  • 1
    @user1211476: Not much clearer, no. The lilac quadrilateral on top looks flat, since no subdivision into triangles is visible. But as I stated above, and as Blue stated in both his comment and his answer, for the numbers you gave us the top quadrilateral cannot be flat. So the image does not fit your numbers. – MvG Jul 08 '13 at 16:10
  • I know, top pane is not flat, you can imagine it as a solid rock with base as square. I think i wont get exact volume but near by exact, using sum calculas/integral. As per my knowledge goes, there are two ways to get volume. Either use formula of cross section, use integral for base area and varies from 0 to max height. Or some how divide given pane into known geometric figure. I am stuck/confuse and dont know how to go ahead with this. if you can throw some light, may be i can proceed. – user1211476 Jul 09 '13 at 10:21
1

It appears that @Blue and @MvG have landed on the same formula which I believe is correct. I came up with the same formula using calculus. It can be described by "Area of the base times the average height". The calculus is done by extruding a right trapezoid in the XY plane along the Z axis, where the heights of the sides are described by $y_0$ and $y_1$

$$\begin{align}y_0 &= a(z) = \Biggl(\frac{{y_a}_f - {y_a}_i}{L}\Biggr)z + {y_a}_i\\\\y_1 &= b(z) = \Biggl(\frac{{y_b}_f - {y_b}_i}{L}\Biggr)z + {y_b}_i\\\\A &= \frac{W}{2}(y_0 + y_1)\\\\&=\frac{W}{2}[a(z) + b(z)]\\\\V &= \int^L_0A(dz)\\\\&=\frac{W}{2}\int^L_0[a(z) + b(z)](dz)\\\\&NOTE: \,\,\,\, a(0) = b(0) = 0\\\\&=\frac{W}{2}\Biggl[\frac{({y_a}_f - {y_a}_i)z^2}{2L} + {y_a}_iz + \frac{({y_b}_f - {y_b}_i)z^2}{2L} + {y_b}_iz\Biggr]\\\\&= \frac{W}{2}\Biggl(\frac{z}{2L}\Biggr)\Biggl[({y_a}_f - {y_a}_i)z + 2L{y_a}_i + ({y_b}_f - {y_b}_i)z + 2L{y_b}_i\Biggr]\\\\&Evaluate\,\,\,at\,\,\,z = L\\\\&= \frac{WL^2}{4L}({y_a}_f - {y_a}_i + 2{y_a}_i + {y_b}_f - {y_b}_i + 2{y_b}_i)\\\\&= \frac{WL}{4}({y_a}_f + {y_a}_i + {y_b}_f + {y_b}_i)\\\\&=\frac{WL}{4}\sum h \\\\&\Rightarrow WL\frac{\sum h}{4}\\\\&= Area\,\,\,of\,\,\,base\,\,\,(WL)\,\,\,times\,\,\,average\,\,\,height\,\,\,\Biggl(\frac{\sum h}{4}\Biggr)\end{align}$$

Right trapezoid math figures

Mark Davich
  • 136