P-adic Number Expansions and Least Residue Systems

Question

My basic question that will relate to what I write here after is this: Is there any incorrect statements I have made in my description of the mathematics shown?

We start again with the Kronecker delta:

$$\delta \left( x,y \right) =\cases{1&$x=y$\cr 0&$x\neq y$\cr}\quad\qquad\quad\qquad\quad\qquad\quad\qquad\quad\qquad\quad\qquad\quad\qquad\quad\quad\quad\quad\quad\quad\quad\text{ (1)}$$

Which allows us to express the digits of a number 'a' in base 'b' in a computable integer sequence, in that we already know the exact length of the sequence which is of course the number of digits in total. The expression for this computation is:

$$d_{{n}} \left( a,b \right) =\sum _{k=1}^{ \Bigl\lfloor {\frac { \ln \left( a \right) }{\ln \left( b \right) }}\Bigr\rfloor +1} \left( \delta \left( n,k \right) -b\delta \left( n,k+1 \right) \right) \Bigl\lfloor{a{b}^{k- {\Bigl\lfloor\frac {\ln \left( a\right) }{\ln \left( b \right) }\Bigr\rfloor} -1}} \Bigr\rfloor \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$$

$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\qquad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{ (2)}$$

For example, $a=12345$ in base $b=10:$ will, purely coincidentally of course, evaluate to the arithmetic progression with initial value of 1 and d=1 of length 5: $$\left\{ d_{{1}} \left( 12345,10 \right) ,d_{{2}} \left( 12345,10 \right) ,d_{{3}} \left( 12345,10 \right) ,d_{{4}} \left( 12345,10 \right) ,d_{{5}} \left( 12345,10 \right) \right\} = \left\{ 1,2,3,4, 5 \right\} $$

But this(2) will compute the $n^{th}$ digit for the number in any base $b>1$, and thus these values correspond to the coefficients of the b-adic expansion * of the number thus we have as follows:

$$\mathcal{P} \left( a,b \right) =\sum _{n=0}^{ \Bigl\lfloor { \frac {\ln \left( a \right) }{\ln \left( b \right) }} \Bigr\rfloor +1}d_{ {n}} \left( a,b \right) {b}^{n}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{ (3)} $$ Additionally, we may also use (2) for the calculation of the p adic valuation of the factorial of a number N for a prime p as follows:

$${\sum _{k=1}^{ \Bigl\lfloor {\frac {\ln \left( N \right) }{\ln \left( p \right) }} \Bigr\rfloor +1} \Bigl\lfloor {\frac {N}{{p}^{k}} } \Bigr\rfloor =\frac {N}{p-1}}-\frac{\sum _{j=1}^{ \Bigl\lfloor {\frac {\ln \left( N \right) }{\ln \left( p \right) }} \Bigr\rfloor +1}d \left( N,p,j \right)}{ \left( p-1 \right) }\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{ (4)}$$

And the lemma below I include for the reader to see my justification for the result stated in (6): where $ \text{There exists}\quad \alpha{\in \Bbb N}\quad\text{and}\quad\beta{\in \Bbb N}\quad\text{such that:}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad $ $k \in {\{0,1,2,3,...,\Bigl\lfloor { \frac {\ln \left( a \right) }{\ln \left( \beta \right) }} \Bigr\rfloor\}}$ and $\alpha\in {\{\beta}^{k}\}$ $$\alpha\,\frac{\mathcal{P} \left( {\frac {\mathcal{P} \left( a,\beta \right) }{\beta}},\beta \right)} {\beta}=a\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{(5)} $$

Because of this almost "periodic" nature of an iteration of (3) returning us the original number in it's original base representation, I believe this to be why when any value greater that 1 is taken for b up to infinity, this recurrence reduces to a finite set under the axiomatic requisite of unique elements of a set to only values that are elements of the least residue system modulo the upper bound of a (N) excluding 0 will occur, thus having been enclosed in a nested set the infinite inner set will reduce to N-1 distinct values which will be those of an arithmetic progression with initial value of 1 and d=1 with total length N-1:

$\text{where } R_N\text{ is the least residue system modulo N:}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$

$ \left\{ \left\{ \frac{\mathcal{P} \left( {\frac {\mathcal{P} \left( a,b \right) }{b}},b \right) }{b} \right\} _{{b={2\ldots \infty }}} \right\} _{{a={1\ldots N-1}}} = R_{{N}} \backslash \left\{ 0 \right\}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{(6)} $

We can then make a declaration of a congruence of $\mathcal{P} \left( a,b \right) $ and 0 modulo the product of $a$ and the base $b$ of the number system for which it is represented in:

$$\mathcal{P} \left( {\frac {\mathcal{P} \left( a,b \right) }{b}},b \right)\equiv 0\pmod {ab}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{(7)} $$

I do however want to note in light of some recent concerning trends on the internet propagated by an individual who I will not name, that this in no way should be misconstrued as the author having a finitist view, this is entirely a consequence of the nature of this particular computation, please do not ask me if this is proof that "numbers have an end".

I have included this enumeration below if the reader is unclear as to what I have attempted to state in (4), as I do not know the formal terminology for describing this observed pattern.

$$\quad\,\mathcal{P} \left( \frac{1}{2}\,\mathcal{P} \left( 12,2 \right) ,2 \right) =12 $$ $$\quad\frac{1}{2}\mathcal{P} \left( \frac{1}{2}\mathcal{P} \left( 123,2 \right) ,2 \right) =123$$ $$\quad\qquad\mathcal{P}\left( \frac{1}{2}\mathcal{P} \left( 1234,2 \right) ,2 \right) = 1234\quad$$ $$\quad\quad\frac{1}{2}\,\mathcal{P} \left( \frac{1}{2}\mathcal{P} \left( 12345,2 \right) ,2 \right) =12345\quad$$

$$32\,\mathcal{P} \left( \frac{1}{2}\mathcal{P} \left( 123456,2 \right) ,2 \right) =123456 $$

$$\frac{1}{2}\mathcal{P} \left( \frac{1}{2}\mathcal{P} \left( 1234567,2 \right) ,2 \right) =1234567 $$

An additional note to make would be that one can clearly see this approach can be used to compute the digital root of a number or more readily the sum it's digits in any base, which has an intimate relationship with the p-adic order of the number, which I encourage the reader's review of here

I will end at this point to await feedback, seeing If anything I have stated above is incorrect, any of the further content on this subject must be brought into question.

Although it follows directly from assuming lemma (4) to be true, for this result I cannot verfiy to sufficiently high values without finding a more efficient means of calculation or purchasing a more powerful computer, so I encourage the reader to attempt to disprove or prove it as I will be, (unless this has already been done):

$$ \left\{ \left\{ \frac{\ln \left( \frac{a}{ \left( \mathcal{P} \left( {\frac {\mathcal{P} \left( a, \beta \right) }{\beta}},\beta \right) \right)} \right)}{ \left( \ln \left( \beta \right) \right) }+1 \right\} _{{a={1\ldots \infty }}} \right\} _{{\beta={2 \ldots \infty }}}=R_{{9}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{(8)} $$

It quite possibly can be explained by the fact that this is the least residue system for the number of distinct digits used in our number system, but so far everything here has been derived under the author's assumption that theoretically the base of the chosen number system can be any fixed natural number greater than 1, so if this were to be calculated in a number system of a higher base, we would obtain a least residue system of a correspondingly higher order, that is to say:

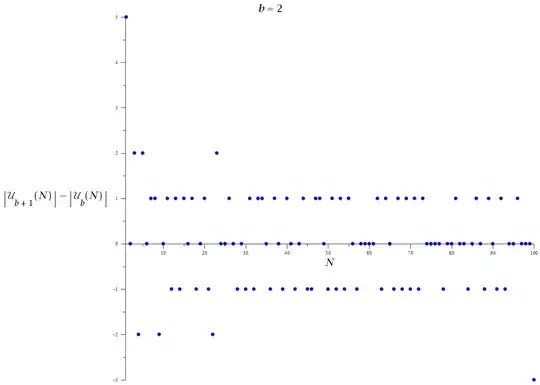
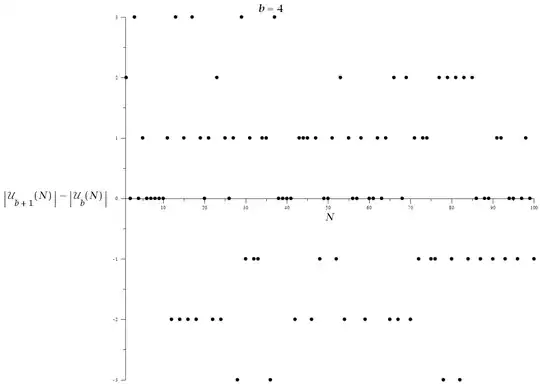
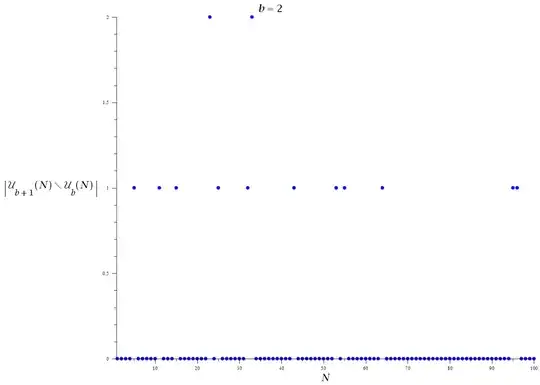
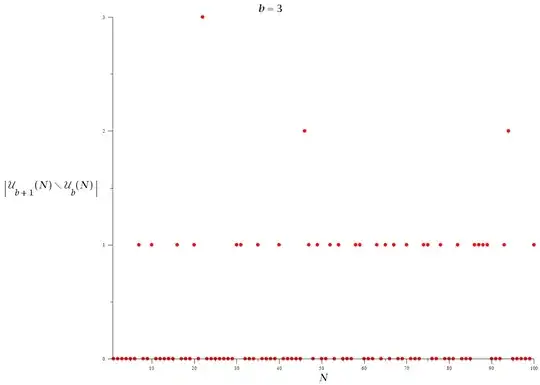
Defining $\mbox {U}_{{b}} \left( N \right) $ as the intersection of all of the digit sets D of all divisors of a number N over all number bases less than or equal to it's number base b:

$U_b(N)=\bigcap^{b}_{\beta=2}\bigcap^{\tau(N)}_{j=1}D(p_{N,b,j}^{v_{N,b,j}},\beta)$

The following distributions show the variance in the quantity with respect to N (first two plots) and the variance between consecutive values of b (last three plots):

Answer 1

(Caution: much of the below is my opinion, but I feel comfortable in saying that it's generally the 'common opinion' of the mathematical community.)

I think there's a misconception at work here that the goal of mathematics is to provide explicit formulas for things. Formulas can be a useful means to an end, but they are not an end in and of themselves; the ultimate goals of mathematics are to be able to understand mathematical structures and to be able to communicate understanding of those structures; a formula is useful insomuch as it provides either understanding or a useful means of communication.

Perhaps the canonical (negative) example of this is the explicit formulas for the prime numbers. For instance, by Wilson's formula, we have $(n-1)!+1$ exactly divisible by $n$ iff $n$ is prime (or $1$, of course), so $\left\lfloor\cos^2\left(\pi\dfrac{(n-1)!+1}{n}\right)\right\rfloor$ will be equal to $1$ iff $n$ is either $1$ or prime; this means that we can write the prime-counting function $\pi(n)$ as $\displaystyle \pi(n)=\sum_{j=2}^n\left\lfloor\cos^2\left(\pi\dfrac{(j-1)!+1}{j}\right)\right\rfloor$. But no meaningful discovery about the primes has come out of this formula! There's no structure in it; the pieces don't really cohere, and they're not especially amenable to deeper analysis.

By contrast, consider the explicit formula for the Fibonacci numbers $F_n=\dfrac{\phi^n-\bar{\phi}^n}{\phi-\bar{\phi}}$ (where $\phi=\frac12(1+\sqrt{5})$ is the golden ratio and $\bar{\phi}=\frac12(1-\sqrt{5})=-\phi^{-1}$ is its 'conjugate'). On the surface, it's not even clear that this should be an integer — but there's a lot of structure in this formula. Not only does it tell us exactly how fast the sequence grows (exponentially, with order of growth $\phi$) but we can also use it to prove things like the divisibility property $F_n|F_{mn}$ for all $m,n$ (since $\dfrac{F_{mn}}{F_n}=\dfrac{\phi^{mn}-\bar{\phi}^{mn}}{\phi^n-\bar{\phi}^n} = \sum_i\phi^{in}\bar{\phi}^{(m-i)n}$ and we can show that the latter expression is an integer); what's more, we can extend these results to general linear relations of the form $P_n=dP_{n-1}+P_{n-2}, P_0=0, P_1=1$ (with some small constraints on $d$) because all of these relations satisfy a formula with a nearly identical structure.

As things stand, the formulas that you've presented seem very much more akin to the explicit prime formulas than to the explicit formula for the Fibonaccis. Having an explicit formula for the digits of a number isn't a bad thing, but it still leaves the question: what understanding, or what communication, does it grant? I would contend that the formulas you've come up with are no better at expressing the notion of '$n$th digit of a number' than that phrase itself, and more to the point, they're no more rigorous than the usual definition. You need to show what your formula can do that can't be done with the usual definitions.