Show that $\left(\sum_{r=1}^n r\right)^2=\sum_{r=1}^n r^3$ without expanding to closed form

Question

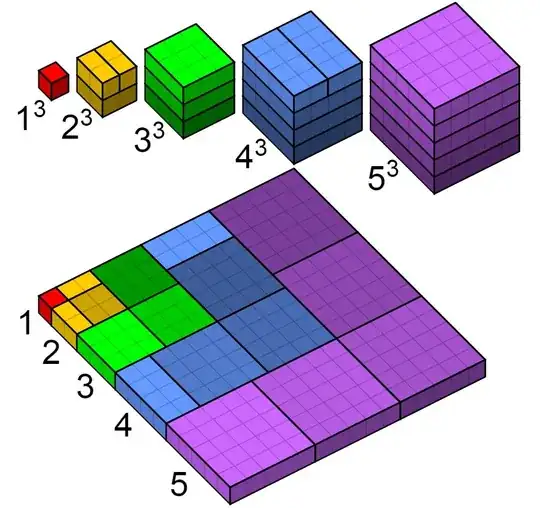
It is well know that $$\left(\sum_{r=1}^n r\right)^2=\sum_{r=1}^n r^3$$ i.e. $$(1+2+3+\cdots+n)(1+2+3+\cdots+n)=1^3+2^3+3^3+\cdots+n^3$$ and this is usually proven by showing that the closed form for the sum of cubes is $\frac 14 n^2(n+1)^2$ which can be written as $\left(\frac 12 n(n+1)\right)^2$, and then noticing that $\frac 12 n(n+1)$ is the sum of integers.

Is it possible to prove the result, preferably from LHS to RHS, without first expanding the summation to closed form, as described above?

Note: The intention is to arrive at RHS from LHS by manipulation of limits and summands without full expansion to closed form, rather than using induction, or graphical methods, like Nicomachus' method.

Answer 1

The graphical proof can be turned into a manipulation of the sum, but at some point you do still have to use the formula for the sum $1 + 2 + \dots +k$.

\begin{align*} \left(\sum_{r=1}^n r\right)^2 &= \left(\sum_{i=1}^n i\right)\left(\sum_{j=1}^n j\right) \\ &= \sum_{i=1}^n \sum_{j=1}^n ij \\ &= \underbrace{\sum_{i=1}^n \sum_{j=1}^{i} ij}_{i\ge j \text{ terms}} + \underbrace{\sum_{j=1}^n \sum_{i=1}^{j-1} ij}_{i<j \text{ terms}} \\ &= \sum_{r=1}^n \left(\sum_{s=1}^r rs + \sum_{s=1}^{r-1} rs \right) \\ &= \sum_{r=1}^n r \left(\sum_{s=1}^r s + \sum_{s=1}^{r-1} s \right) \\ &= \sum_{r=1}^n r \left(\frac{r(r+1)}{2} + \frac{r(r-1)}{2}\right) = \sum_{r=1}^n r^3. \end{align*}

---

Actually, with a final trick, we can do without any formulas entirely. Starting midway through the above proof, continue instead with \begin{align*} \left(\sum_{r=1}^n r\right)^2 &= \sum_{r=1}^n \left(\sum_{s=1}^r rs + \sum_{s=1}^{r-1} rs \right) \\ &= \sum_{r=1}^n \left( \sum_{s=1}^r rs + \color{red}{\sum_{s=1}^{r} r(r-s)} \right) \\ &= \sum_{r=1}^n \sum_{s=1}^r r[s + (r-s)] \\ &= \sum_{r=1}^n \sum_{s=1}^r r^2 = \sum_{r=1}^n r^3 \end{align*}

where the highlighted manipulation is just reversing the order in which we're summing $r + 2r + \dots + r(r-1)$, extended with an extra $r\cdot 0$ term at the end to make the two sums match.

Answer 2

proof without words

from: (https://upload.wikimedia.org/wikipedia/commons/2/26/Nicomachus_theorem_3D.svg)

Answer 3

$$ \underbrace{(1+2+3+\cdots+n)(1+2+3+\cdots+n) = 1^3+2^3+3^3+\cdots+n^3}_{\Large\text{This will be our induction hypothesis.}} $$ \begin{align} & \Big( \underbrace{1+2+3+\cdots+n}_{\Large A} +\underbrace{\Big(n+1\Big)}_{\Large B}~~\Big)^2 \\[10pt] = {} & (A+B)^2 = A^2+2AB+B^2 \\[10pt] = {} & \overbrace{(1+2+3+\cdots+n)^2}^{\Large A^2} {}+{} \overbrace{2(1+2+3+\cdots+n)(n+1)}^{\Large 2AB} + \overbrace{(n+1)^2}^{\Large B^2} \\[10pt] = {} & \Big(1^3+2^3+3^3+\cdots+n^3\Big) + 2(1+2+3+\cdots+n)(n+1) + (n+1)^2 \\ & \quad \text{by the induction hypothesis} \\[10pt] = {} & \Big(1^3+2^3+3^3+\cdots+n^3\Big) + \Big(n(n+1)\Big)(n+1) + (n+1)^2 \\ & \quad \text{(since $1+2+3+\cdots+n = \dfrac {n(n+1)} 2$)} \\[10pt] = {} & \Big(1^3+2^3+3^3+\cdots+n^3\Big) + (n+1)^3. \end{align}

Answer 4

By induction:

You have to know the high-school formula $\;\displaystyle\sum_{r=1}^n r=\frac{n(n+1)}2$.

Suppose $\;\Bigl(\displaystyle\sum_{r=1}^n r\Bigr)^2=\sum_{r=1}^n r^3 $ for some $n\ge 1$. Then \begin{align} \Bigl(\mkern1mu\sum_{r=1}^{n+1} r\Bigr)^2&=\Bigl(\displaystyle\sum_{r=1}^n r\Bigr)^2+2(n+1)\sum_{r=1}^{n+1} r+(n+1)^2\\ &=\sum_{r=1}^n r^3 + n(n+1)^2+(n+1)^2&\text{by inductive hypothesis}\\ &=\sum_{r=1}^n r^3 +(n+1)(n+1)^2=\sum_{r=1}^{n+1} r^3. \end{align}

Answer 5

This was the answer I had derived and is posted for information only. It is similar to the answer just posted by Misha Lavrov.

$$\begin{align} \left(\sum_{r=1}^n r\right)^2&= 2\sum_{r=1}^n\sum_{s=r}^n rs-\sum_{r=1}^n r^2\\ &=2\sum_{s=1}^n\sum_{r=1}^s rs-\sum_{r=1}^n r^2\\ &=2\sum_{s=1}^n s\binom {s+1}2-\sum_{s=1}^n s^2\\ &=\sum_{s=1}^ns^2(s+1)-s^2\\ &=\sum_{s=1}^n s^3=\sum_{r=1}^n r^3\end{align}$$

As Misha pointed out, this uses the fact that $\displaystyle\sum_{r=1}^s r=\frac {s(s+1)}2$, which seems unavoidable (although the summation is an intermediate evaluation and is summed to $s$ rather than to $n$). However, it does not use the closed form of $\displaystyle\sum_{r=1}^n r^3=\frac {n^2(n+1)^2}4$. It would be interesting to see if it is possible to come up with a proof without using both.

Answer 6

Lemma: If $f(x,y)$ is a binary function, then: $$\sum_{i=1}^{n} \sum_{j=1}^{n} f(i,j)=\sum_{k=1}^{n} \left(f(k,k)+\sum_{i=1}^{k-1}f(i,k)+\sum_{j=1}^{k-1}f(k,j)\right)$$

The graphical proof can be written starting with $f(x,y)=1$ to show:

$$n^2=n+\sum_{k=1}^{n}(k-1)+\sum_{k=1}^{n}(k-1)=n+\sum_{i=1}^{n-1}i +\sum_{j=1}^{n-1}j$$

Thus:

$$n^3=n\left(n+\sum_{i=1}^{n-1} i+\sum_{j=1}^{n-1}j\right)$$

And $$\begin{align}\sum_{k=1}^{n} k^3 &= \sum_{k=1}^{n} \left(k\cdot k +\sum_{i=1}^{k}i\cdot k + \sum_{j=1}^{k}k\cdot j\right)\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n} i\cdot j\text{ (using lemma with $f(x,y)=xy$)}\\ &=\left(\sum_{i=1}^{n}i\right)\left(\sum_{j=1}^{n} j\right)\\ &=\left(\sum_{i=1}^{n}i\right)^2 \end{align}$$

---

So, amusingly, while we have shown that $2\sum_{k=1}^{n-1} k = n^2-n$, we aren't using that identity in the place where you'd expect - we use it to decompose $n^3$.

---

The inductive approach is to prove:

$$(1+2+\cdots+n+(n+1))^2-(1+2+\cdots+n)^2=(n+1)^3$$

The difference of two squares gives the left side equal to:

$$\begin{align}(n+1)((1+\cdots+n)+(n+\cdots+1)+(n+1))&=(n+1)(n(n+1)+n+1)\\ &=(n+1)^3\end{align}$$

This is essentially the same proof.