Finding an asymptotic for the sum $\sum_{p\leq x}p^m$

Question

Possible Duplicate:
How does $ \sum_{p \leq x} p^{-s} $ grow asymptotically for $ \text{Re}(s) < 1 $?

What could I use to prove the following conjecture?

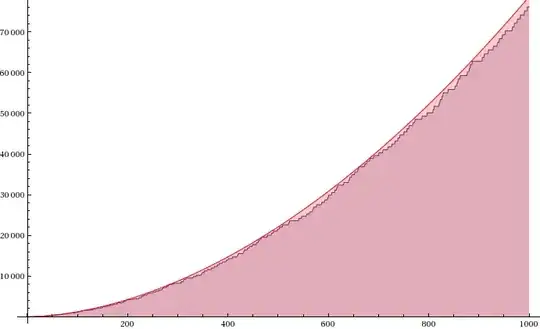
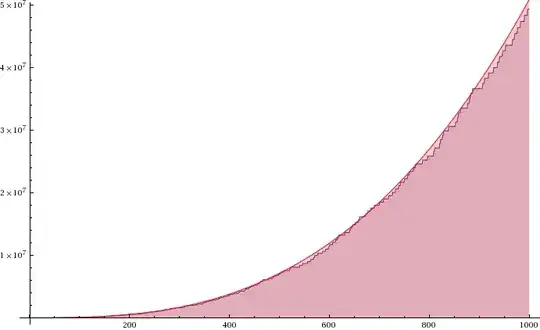
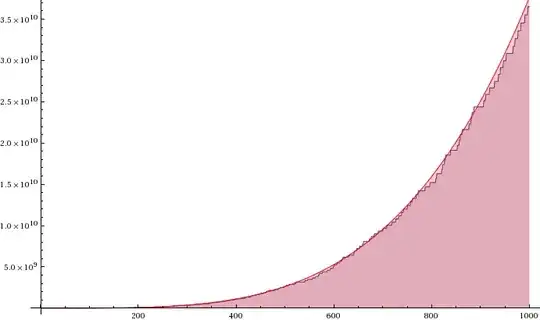
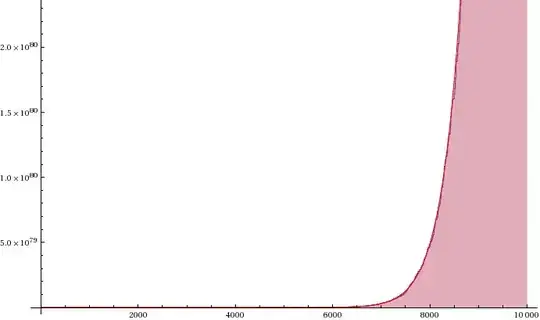
$ \sum_{p \le x} p^{m} \sim \operatorname{Li}(x^{m+1}) $

For $ m=0 $ this is just the prime number theorem, but would it be true for other numbers 'm' ? Or even for negative m?

Also if the function can be expanded in power series $ f(x)= \sum_{n=0}^{\infty} a(n)x^{n} $,

I also think that $ \sum _{p \le x}f(x) \sim \sum_{n=0}^{\infty}a(n)\operatorname{Li}(x^{n+1}) $.

Of course $ \operatorname{Li}(x)= \int_{2}^{x}\frac{du}{\ln(u)} $.

Answer 1

This is not an answer but a plot for $m=1,2,3,10,20$ because some peopel asked for that.

EDIT: This is somewhat an answer now, see below.

I entered the following code in Mathematica:

m = 1
maxx = 100
p1 = DiscretePlot[Sum[Prime[n]^m, {n, PrimePi[x]}], {x, maxx}];
p2 = DiscretePlot[LogIntegral[x], {x, maxx}, PlotStyle -> Red];
Show[{p1, p2}]

It seems alright for small $m$, as you can see below.

---

Okay, so in this paper we find that: $$\sum_{p\leq x\text{ prime}}f(p)\approx\int_2^x \frac{f(y)dy}{\ln y}$$

Substituting $f(p)=p^m$ gives, according to wolfram alpha: $$\sum_{p\leq x\text{ prime}}p^m\approx \text{Ei}((n+1)\ln x)= \text{Ei}(\ln x^{n+1})=\text{Li}(x^{n+1})$$

---

$m=1$ $m=2$ $m=3$ $m=10$ $m=20$, $maxx=10000$