1

enter image description here

This is Rudin's functional Analysis chapter $10$, exercise $13$.

I am confused about the notation $\sigma_A(f)$, what does that mean?(What role does the subscript $A$ play here). And can someone illustrate how to solve this question?

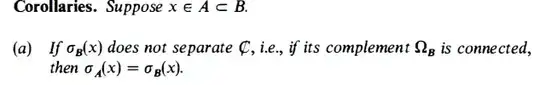
Update: thanks to the comment, and a theorem in Rudin: enter image description here

$B$ is the collection of polynomials of $x$ ($|x| \in [1,2]$), whose power ranges from negative to positive. So the only possible $\lambda$ (here I use $\lambda$ to denote the spectral, while $x$ as variable in the function, not the way in the question) is 1.

Actually, if we want $(\lambda*e-f)(x) *P(x)=1$ when $\lambda$ is not $1$, we can simply choose $P(x)$ to be $\frac{1}{(\lambda-1)x}$.

So by the theorem in Rudin, $\sigma_A=\sigma_B={1}$.

Is this correct?

Toad Jiang
  • 977
  • it seems there is a special notion of spectrum in a Banach algebra : https://en.wikipedia.org/wiki/Banach_algebra#Spectral_theory and $\sigma_A(T)$ would be the set such that $z \in \sigma_A(T) \Leftrightarrow (T-zI)^{-1} \not \in A$ – reuns Apr 22 '16 at 05:49
  • If $B$ is a subalgebra, by the definition of algebra(by folland, if $A$ is an algebra, $f,g \in A$, $\implies f*g \in A$),can we say that $1$ is also in $B$, which implies $A \subset B$? – Toad Jiang Apr 22 '16 at 19:04
  • yes if $B$ contains $f$ and $1/f$ it clearly contains $f (1/f) = 1$. in the context of Banach algebras, you should think to sub vector spaces of the space of matrices $\mathbb{C}^{n \times n}$ closed for the multiplication of matrices, and with the usual matrix norm $|M| = \max_{|x|=1} |Mx|$ (with $|x|$ the Euclidean norm), then you get the same kind of objects when considering the algebra of bounded linear operator from an Hilbert space to itself, with again the operator norm, and the sub vectors paces which are closed for the composition of operators. – reuns Apr 22 '16 at 19:13
  • and remember that an algebra is the basic structure where we can consider the set of polynomials $P(T) =\sum_{k=1}^K c_k T^k$ where $T$ is any element of the algebra, and $c_n$ the constants of the underlying field of the vector space – reuns Apr 22 '16 at 19:14
  • 1
    Write $\sigma(f)$ for the spectrum of $f$ in $C(K)$. Note that $\alpha\in\sigma(f) \iff \alpha-f$ is not invertible, and this is equivalent to say that $\alpha - \lambda$ is not invertible for some $\lambda\in K$, which means that $\alpha \in K$. Therefore, $\sigma(f) = K$. Now, remember that $\sigma_A(f) \supset \sigma_B(f) \supset \sigma(f) = K$, so it's not possible to have $\sigma_A(f)$ or $\sigma_B(f)$ equal to $1$.

    PS: I'm using Rudin's notation, $f(\lambda) = \lambda$.

     – Integral Apr 22 '16 at 23:59
  • @Integral Can you explain how do you conclude that $\sigma(f)=K$? – Toad Jiang Apr 23 '16 at 02:57

0 Answers0