$\DeclareMathOperator{\Span}{span} \newcommand{\R}{\mathbf R} \newcommand{\mc}{\mathcal} \DeclareMathOperator{\GL}{GL} \DeclareMathOperator{\grassman}{GR} \newcommand{\set}[1]{\{#1\}} \DeclareMathOperator{\id}{Id}$ I had previously asked here if there is a neat way to prove that the Grassmannian manifold is Hausdorff (without using matrices). Olivier Begassat gave a nice answer which uses a clever idea endowing the vector space with an inner product. There were other interesting answers too.
I now have a more basic proof of the same statement which I would like to share. I hope this will be useful to the reader.
Definition. Let $V$ be an $n$-dimensional vector space. A $k$-frame in $V$ is an injective linear transformation $T:\R^k\to V$. The set of all the $k$-frames of $V$ is written as $F_k(V)$.
It is clear that $F_k(V)$ is an open subset of $\mc L(\R^k, V)$ and is therefore a $kn$-dimensional manifold.
We define an equivalence relation $\sim$ on $F_k(V)$ as follows: Given two $k$-frames $S$ and $T$ in $V$, we write $S\sim T$ if and only if $T(\R^k)=S(\R^k)$. It is clear that $\sim$ is an equivalence relation on $F_k(V)$. Note that $T\sim S$ for $T, S\in F_k(V)$ if and only if there exists $\tau\in \GL_k(\R)$ such that $S=T\circ \tau$.
Definition. We define the Grassmannian manifold $\grassman_k(V)$ as the quotient space $F_k(V)/\sim$.
Remark. Note that $\R^k$ is in no way special here. We could have chosen any $k$ dimensional linear space. It can be easily seen that the Grassmannian remains undisturbed either as a set or a topological space under this change. We will make use of this flexibility shortly.
We now set out to prove that the Grassmannian manifold is Hausdorff. We require some ground work to do that.
Define $\pi:F_k(V)\to\grassman_k(V)$ as the projection map, that is, $\pi$ carries $T$ to the equivalence class of $T$
Theorem 1. The projection map $\pi:F_k(V)\to \grassman_k(V)$ as defined above is an open map.
Proof.
Let $U$ be open in $F_k(V)$. We need to show that $\pi(U)$ is open in $\grassman_k(V)$, for which we need to show that $\pi^{-1}(\pi(U))$ is open.
Let $T\in \pi^{-1}(\pi(U))$.
Thus $\pi(T)\in \pi(U)$, which is equivalent to saying that $T=S\circ \tau$ for some $S\in U$ and $\tau\in \GL_k(\R)$.
Define a map $f_\tau:F_k(V)\to F_k(V)$ as $f_\tau(L)=L\circ \tau$ for all $L \in F_k(V)$.
learly $f_\tau$ is continuous with $f_{\tau^{-1}}$ being a continuous inverse to it.
Therefore, $f_\tau$ is a homeomorphism, and we deduce that $f_\tau(U)$ is open in $F_k(V)$.
Now we have $T\in f_\tau(U)$ and $f_\tau(U)\subseteq \pi^{-1}(\pi(U))$, showing that $\pi^{-1}(\pi(U))$ is open, and consequently $\pi$ is an open map.
For any given $(n-k)$-dimensional subspace $A$ of $V$, let $\mc U_A$ denote the set of all the $k$-dimensional subspaces of $V$ which intersect $A$ trivially. Thus for any member $B\in \mc U_A$, we have $V=A\oplus B$.
Lemma 2.
Given an $(n-k)$-dimensional subspace of $V$, the set $\mc U_A$ is open in $\grassman_k(V)$.
Proof. Write $m=n-k$ and fix a basis $u_1 , \ldots, u_m$ of $A$.
For a member $T\in F_k(V)$, $\pi(T)$ intersects $A$ trivially if and only if $(u_1 \wedge \cdots \wedge u_m)\wedge(T\mathbf e_1 \wedge \cdots \wedge T\mathbf e_k)\neq 0$.
So we define a function $f:F_k(V)\to \Lambda^k V$ as
\begin{equation*}
f(T) = (u_1 \wedge \cdots \wedge u_m)\wedge(T\mathbf e_1 \wedge \cdots \wedge T\mathbf e_k)\neq 0
\end{equation*}
Thus $\pi(T)\in \mc U_A$ if and only if $f(T)\neq 0$ if and only if $T\in f^{-1}(\Lambda^k V-\set{0})$.
herefore,
\begin{equation*}
\mc U_A=\textstyle\pi(f^{-1}(\Lambda^k V-\set{0}))
\end{equation*}
Now $f$ is continuous (smooth, even) because it is a restriction of a linear map on $\mc L(\R^k, V)$ to the open subset $F_k(V)$ of $\mc L(\R^k, V)$
Using the fact that $\pi:F_k(V)\to \grassman_k(V)$ is open, we see that $\mc U_A$ is open in $\grassman_k(V)$.
Definition. Let $P$ and $Q$ be $k$ and $n-k$ dimensional subspaces of $V$ respectively such that $V=P\oplus Q$. Given any linear map $T:P\to Q$, the graph $\Gamma(T)$ of $T$ is defined as $$ \Gamma(T)=\set{x+Tx:\ x\in P} $$
Lemma 3. Let $A$ be an $(n-k)$-dimensional subspace of $V$ and $B$ be a $k$-dimensional subspace of $V$ which intersects $A$ trivially.
Then $\mc U_A$ is homeomorphic to $\mc L(B, A)$.
Proof. To prove this, we think of frames as injective linear maps from $B$ to $V$.
Let $p_{A, B}:V\to A$ be the projection onto $A$ with respect to $B$ and similarly we have $p_{B, A}$.
Note that for any $T\in \pi^{-1}(\mc U_A)$, we have $p_{B, A}\circ T:B\to B$ is a linear isomorphism.
Define a function $\Phi:\pi^{-1}(\mc U_A)\to \mc L(B, A)$ as $\Phi(T)=\Phi_T$, where the latter is defined as
\begin{equation*}
\Phi_T(x) = (p_{A, B}\circ T)\circ (p_{B, A}\circ T)^{-1}(x)
\end{equation*}
for all $x\in B$.
It can be shown that $\Phi_T=\Phi_S$ if and only if $\pi(T)=\pi(S)$ and that $\Phi$ is surjective.
Since $\pi$ is a quotient map, we get a bijective continuous map $\bar\Phi:\mc U_A\to \mc L(B, A)$ such that the following diagram commutes
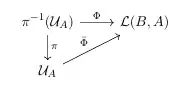
We now show that $\bar \Phi$ is a homeomorphism by constructing an inverse.
Define $g:\mc L(B, A)\to \mc U_A$ as $g(S)=\Gamma(S)$, that is, $g$ takes $S$ to its graph in $V$.
Let $B'\in \mc U_A$ be arbitrary and let $T:B\to V$ be defined as the restriction of $p_{B', A}:V\to B'$ to $B$.
Then it is easy to check that $\pi(T)=B'$ and thus $T\in \pi^{-1}(\mc U_A)$.
Therefore $\bar \Phi(B')=\Phi(T)$ and it can be easily checked that $\Gamma(\Phi(T))=B'$, showing that $g\circ \bar\Phi=\id$ and we are done.
Theorem 4. The Grassmannian $\grassman_k(V)$ is Hausdorff.
Proof. Let $B$ and $B'$ be any two distinct members of $\grassman_k(V)$. We can find an $(n-k)$ -dimensional subspace $A$ of $V$ which intersects both $B$ and $B'$ trivially. Now we use Lemma 3 and the Hausdorffness of $\mc L(B, A)$ to finish.